 设为首页
设为首页
 加入收藏
加入收藏
例1:直线
![]() 过点
过点 ![]() (-1,3),倾斜角的正弦是
(-1,3),倾斜角的正弦是 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
分析:根据倾斜角的正弦求出倾斜角的正切,注意有两解.
解:因为倾斜角 ![]() 的范围是:
的范围是: ![]()
又由题意: ![]() ,
,
所以: ![]() ,
,
直线过点 ![]() (-1,3),由直线的点斜式方程得到:
(-1,3),由直线的点斜式方程得到:
![]()
即: ![]() 或
或 ![]() .
.
说明:此题是直接考查直线的点斜式方程,在计算中,要注意当不能判断倾斜角 ![]() 的正切时,要保留斜率的两个值,从而满足条件的解有两个.
的正切时,要保留斜率的两个值,从而满足条件的解有两个.
例2:求经过两点
![]() (2,
(2, ![]() )和
)和 ![]() (
( ![]() ,3)的直线方程.
,3)的直线方程.
分析:本题有两种解法,一是利用直线的两点式;二是利用直线的点斜式.在解答中如果选用点斜式,只涉及到 ![]() 与2的分类;如果选用两点式,还要涉及
与2的分类;如果选用两点式,还要涉及 ![]() 与3的分类.
与3的分类.
解:法一:利用直线的两点式方程
∵直线过两点 ![]() (2,
(2, ![]() )和
)和 ![]() (
( ![]() ,3)
,3)
(1)当 ![]() 时,点
时,点 ![]() 的坐标是
的坐标是 ![]() (2,3),与点
(2,3),与点 ![]() (
( ![]() ,3)的纵坐标相等,则直线
,3)的纵坐标相等,则直线
![]() 的方程是
的方程是 ![]() ;
;
(2)当 ![]() 时,点
时,点 ![]() 的坐标是
的坐标是 ![]() (2,3),与点
(2,3),与点 ![]() (2,
(2, ![]() )的横坐标相等,则直线
)的横坐标相等,则直线
![]() 的方程是
的方程是 ![]() ;
;
(3)当 ![]() ,
, ![]() 时,由直线的两点式方程
时,由直线的两点式方程 ![]() 得:
得:
![]()
法二:利用直线的点斜式方程
(1)当 ![]() 时,点
时,点 ![]() 的横坐标相同,直线
的横坐标相同,直线 ![]() 垂直与
垂直与 ![]() 轴,则直线
轴,则直线 ![]() 的
的 ![]() ;
;
(2)当 ![]() 时,过点
时,过点 ![]() 的直线的斜率是
的直线的斜率是 ![]() ,
,
又∵过点 ![]() (2,
(2, ![]() )
)
∴由直线的点斜式方程 ![]() 得过点
得过点 ![]() 的直线的方程是:
的直线的方程是:
![]()
说明:本题的目的在于使学生理解点斜式和两点式的限制条件,并体会分类讨论的思想方法.
例3:把直线方程
![]() 化成斜截式_________,化成截距式__________.
化成斜截式_________,化成截距式__________.
分析:因为 ![]() ,即
,即 ![]() ,
, ![]() ,
, ![]() ,按斜截式、截距式的形式要求变形即可.
,按斜截式、截距式的形式要求变形即可.
解:斜截式为 ![]() ,截距式为
,截距式为 ![]() +
+ ![]() =1
=1
说明:此题考查的是直线方程的两种特殊形式:斜截式和截距式.
例4:过点
![]() (3,0)作直线
(3,0)作直线 ![]() ,使它被两相交直线
,使它被两相交直线 ![]() 和
和 ![]() 所截得的线段
所截得的线段 ![]() 恰好被
恰好被 ![]() 点平分,求直线
点平分,求直线 ![]() 的方程.
的方程.
解:设 ![]() 点坐标(
点坐标( ![]() ,
, ![]() )
)
![]() 线段
线段 ![]() 的中点为
的中点为 ![]() (3,0)
(3,0)
∴
由中点公式,可设 ![]() 点坐标为
点坐标为 ![]()
![]()
![]() ,
, ![]() 两点分别在直线
两点分别在直线 ![]() 和
和 ![]() 上
上
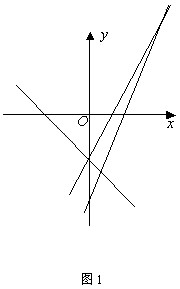
∴
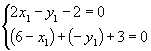
解得 ![]()
由两点式可得直线 ![]() 的方程为:
的方程为: ![]()
例5:一根铁棒在20°时,长10.4025米,在40°时,长10.4050米,已知长度l和温度t的关系可以用直线方程来表示,试求出这个方程,并且根据这个方程,求这跟铁棒在25°时的长度.
解:这条直线经过两点(20,10.4025)和(20,10.4050),根据直线的 两点式方程,得:
![]() =
= ![]()
即
![]() =0.0025
=0.0025 ![]() +10.4000
+10.4000
当
![]() =25°时
=25°时
![]() =0.0025
=0.0025 ![]() +10.4000=0.0031+10.4000=10.4031
+10.4000=0.0031+10.4000=10.4031
即当
![]() =25°时,铁棒长为10.4031米.
=25°时,铁棒长为10.4031米.
说明:直线方程在实际中应用非常广泛.
例6:已知
![]() ,其中
,其中 ![]() 、
、 ![]() 是实常数,求证:直线
是实常数,求证:直线 ![]() 必过一定点.
必过一定点.
分析:观察条件与直线方程的相似之处,可把条件变形为
![]() ,可知
,可知 ![]() ,
, ![]() 即为方程
即为方程 ![]() 的一组解,所以直线
的一组解,所以直线 ![]() 过定点(6,4).此问题属于直线系过定点问题,此类问题的彻底解决宜待学完两直线位置之后较好,当然现在也可以研究,并且也有一般方法.
过定点(6,4).此问题属于直线系过定点问题,此类问题的彻底解决宜待学完两直线位置之后较好,当然现在也可以研究,并且也有一般方法.
例7:直线
![]() 过点
过点 ![]() (2,1),且分别交
(2,1),且分别交 ![]() 轴、
轴、 ![]() 轴的正半轴于点
轴的正半轴于点 ![]() 、
、 ![]() .点
.点 ![]() 是坐标原点,(1)求当
是坐标原点,(1)求当 ![]() 面积最小时直线
面积最小时直线 ![]() 的方程;(2)当
的方程;(2)当 ![]()
![]() 最小时,求直线
最小时,求直线 ![]() 的方程.
的方程.
解:(1)如图,设 ![]()
![]() ,
, ![]()
![]() ,
, ![]() 的面积为
的面积为 ![]() ,则
,则
![]()
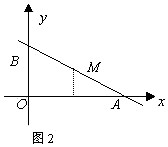 并且直线
并且直线 ![]() 的截距式方程是
的截距式方程是
![]() +
+ ![]() =1
=1
由直线通过点(2,1),得
![]() +
+ ![]() =1
=1
所以:
![]() =
= ![]() =
= ![]()
因为
![]() 点和
点和 ![]() 点在
点在 ![]() 轴、
轴、 ![]() 轴的正半轴上,所以上式右端的分母
轴的正半轴上,所以上式右端的分母 ![]() .由此得:
.由此得:
![]()
![]()
![]()
![]()
当且仅当
![]()
![]() ,即
,即 ![]() 时,面积
时,面积 ![]() 取最小值4,
取最小值4,
这时
![]() ,直线的方程是:
,直线的方程是: ![]() +
+ ![]() =1
=1
即:
![]()
(2)设 ![]() ,则
,则 ![]() =
= ![]() ,
, ![]() =
= ![]() ,如图2,
,如图2,
所以 ![]()
![]() =
= ![]()
![]() =
= ![]()
当 ![]() =45°时
=45°时 ![]()
![]() 有最小值4,此时
有最小值4,此时 ![]() ,直线
,直线 ![]() 的方程为
的方程为 ![]() .
.
说明:此题与不等式、三角联系紧密,解法很多,有利于培养学生发散思维,综合能力和灵活处理问题能力.动画素材中有关于此题的几何画板演示.