第十节 解斜三角形应用举例

典型例题

　　例1．如图所示，在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°，向山顶前进100米后，又从B点测得斜度为45°，设建筑物的高为50米．求此山对于地平面的斜度的倾斜角 ．

　　分析：设山对于地平面的斜度的倾斜角 ，这样可在△ABC中利用正弦定理求出BC；再在△BCD中，利用正弦定理得到关于 的三角函数等式，进而解出 角．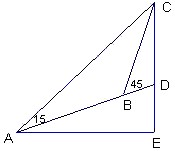

　　解： 在△ABC中， ，

　　

　　

　　根据正弦定理有

　　又在△BCD中，

　　

　　根据正弦定理有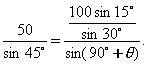

　　解得

　　∴ 山对于地平面的斜度的倾斜角为 ．

　　小结：解应用题，首先要增强应用数学的意识．解应用题可分两步：第一步，先分析问题，抓住实际问题中的数量关系，将其转化成一般数学问题；第二步，利用所学知识和方法解决这个数学问题，其中的关键在于如何将实际问题数学化，也就是说如何将实际问题等价转化成一个数学问题．

　　例2．在一个很大的湖岸边（可视湖岸为直线）停放着一只小船，由于缆绳突然断开，小船被风刮跑，其方向与河岸成15°，速度为 2.5km/h．同时岸上有一人，从同一地点开始追赶小船，已知他在岸上跑的速度为 4km/h，在水中游的速度为 2km/h．问此人能否追上小船？若小船速度改变，则小船能被人追上的最大速度是多少？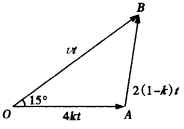

　　分析：由于人在水中游的速度小于船的速度，人只有先沿岸跑一段路程后再游水追赶船，这样才有可能追上，所以本题应讨论的问题不是同一直线上的追及问题．只有当人沿岸跑的轨迹和人游水的轨迹以及船在水中行驶的轨迹它们三者组成一个封闭的三角形时，人才能追上小船．我们可以假设船速为v（未知），人在岸上跑的速度和水中游的速度仍为题目所给定的常数．因人在岸上跑所用的时间与人在水中游所用的时间之和等于船在水中行驶所用的时间，所以当 时，人是不可能追上小船的．当 时，人不必在岸上跑，而立即从同一地点直接下水就可追上小船．因此只有先设法求出它们三者能构成三角形的最大速度 ，再与现有船速进行比较，即可判断人能否追上小船．

　　解：如果我们简单画出此追及情况的示意图（如图所示），设船速为v，人追上船所用时间为t，人在岸上跑的时间为t的k倍 ，则人在水中游的时间应为 ．人要追上船，则人船运动路线满足如图所示的三角形：

　　

　　∴在 中，由余弦定理得：

　　即

　　整理得：

　　

　　要使①式在（0，1）范围内有实数解（在分析中已讨论了 与 的情况，这里考虑 ），则有：

　　

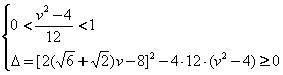
　　解之得：

　　当船速在 内时，人船运动路线可以构成三角形，即人能追上小船．船能使人追上的最大速度为 ，由此可见当船速为 时，人可以追上小船．

　　小结：在上述解题过程中，我们首先是建立了几何模型，即△OAB；其次是通过几何模型的边角关系建立了方程模型，即方程①；最后是根据方程①有解的条件建立了不等式模型．并通过解不等式解答了本问题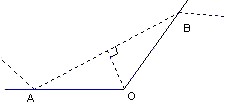．以上解题步骤次序明显，环环相扣．

　　例3．如图，某城市有一条公路从正西方 能过市中心 后转向东北方 ， 在 上设一站 ，在 上设一站 ，铁路在 部分为直线段现要求市中心 与 的距离为10公里，问把 分别设在公路上距中心 多远处才能使 最短，并求其最短距离（不要求作近似计算）

　　解  在 中，设

　　 为正西方向， 为东北方向．

　　

　　 （当且仅当 时，等号成立），又 到 的距离为10，设

　　

　　

　　　

　　 （ ）

　　 因此当 时， 最短，其最短距离为 ，即当 分别在 上离 点 公里处时，能使 最短，其最短距离为 公里．

　　小结：解三角应用题应把握以下几个方面：1）仔细审题，特别是辅助图；2）引入适当的角度（注意角度的范围）；3）解三角形列三角函数式；4）利用有最性求最值．