 设为首页
设为首页
 加入收藏
加入收藏
例1.(1)将点A(5,7),B(2,3)按向量![]() 平移,求平移后各对应点的坐标及向量
平移,求平移后各对应点的坐标及向量![]() 平移后的坐标;
平移后的坐标;
(2)将函数![]() 的图象按向量
的图象按向量![]() 平移,求平移后的图象对应的函数表达式.
平移,求平移后的图象对应的函数表达式.
分析:对于(1),直接运用坐标平移公式便可求得A、B两点平移后对应点的坐标;对于(2),欲求平移后图象对应的函数表达式,就是求![]() 满足的关系式.
满足的关系式.
解:(1)设A、B平移后对应的点分别为![]() ,由平移公式得
,由平移公式得
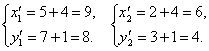
∴对应点![]() ,
,![]() 的坐标分别为(9,8),(6,4).
的坐标分别为(9,8),(6,4).
![]() 平移后为
平移后为![]() ,且
,且![]()
(2)设![]() 是函数
是函数![]() 图象上的任意一点,平移后的对应点为
图象上的任意一点,平移后的对应点为![]() ,那么
,那么
![]()
代入 ![]() ,得
,得 ![]() ,
,
即 ![]() .
.
故欲求的函数表达式为![]() .
.
小结:求平移后的函数表达式,就是求![]() 的关系式,但因为平移后的图象还是在原坐标系xOy中,因此还必须写成x,y的关系式.另外,细心的读者很快可以发现,
的关系式,但因为平移后的图象还是在原坐标系xOy中,因此还必须写成x,y的关系式.另外,细心的读者很快可以发现,![]() 与
与![]() 的坐标相同,你认为是偶然的吗?
的坐标相同,你认为是偶然的吗?
例2.把函数![]() 的图象经过怎样的平移,可以得到函数
的图象经过怎样的平移,可以得到函数![]() 的图象?
的图象?
分析:解题时,只需找到平移前后图象上同一点的坐标之间的关系,就可求出平移向量a.
解:由![]() 可得
可得
![]() .
①
.
①
命 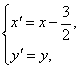 则
则
① 变成
![]() .这与
.这与![]() 相同.
相同.
与平移公式比较可得,![]() .
.
故所求的![]() .
.
小结:利用换元法化简函数解析式是一种常用方法.当所换的变量与原变量之间仅相差一个常数时,这种换元实质上是一个平移变换.
例3.将函数![]() 进行平移,使得到的图形与抛物线
进行平移,使得到的图形与抛物线![]() 的两个交点关于原点对称,求平移后的函数解析式.
的两个交点关于原点对称,求平移后的函数解析式.
分析:本体主要体现平移公式的灵活运用.
解:设平移向量a=(h,k).则将![]() 按a平移后得到的图象的解析式为
按a平移后得到的图象的解析式为![]() ,设
,设![]() 和
和![]() 是
是![]() 与
与![]() 的两个交点,则
的两个交点,则
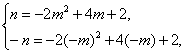 解得
解得 ![]() 或
或 ![]()
∴点(1,4)和点(-1,-4)在函数![]() 的图象上,
的图象上,
∴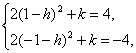 解得
解得 ![]()
故欲求解析式为![]() 即
即![]() .
.
小结:本题的实质是,求抛物线![]() 关于原点对称的图形所对应的函数解析式,利用函数奇偶性的性质也完全可以解决本题,有兴趣的读者不妨一试.
关于原点对称的图形所对应的函数解析式,利用函数奇偶性的性质也完全可以解决本题,有兴趣的读者不妨一试.