 设为首页
设为首页
 加入收藏
加入收藏
例1.已知![]() ,
,![]() ,
,![]() ,
,
求![]() 和
和![]() .
.
分析:运用平面向量数量积的坐标进行计算.
解:![]()
![]()
∴![]() ;
;
![]()
∴![]() .
.
小结:通过本题检验平面向量数量积的运算不具有结合律.
例2.已知两个非零向量![]() 和
和![]() 满足
满足![]() ,求
,求![]() 与
与![]() 的夹角的余弦值.
的夹角的余弦值.
分析:要求![]() 与
与![]() 的夹角的余弦值,首先要确定向量
的夹角的余弦值,首先要确定向量![]() 和
和![]() ,由于已知
,由于已知![]() 是向量的坐标形式,所以运用方程的思想确定
是向量的坐标形式,所以运用方程的思想确定![]() 和
和![]() 的坐标形式.
的坐标形式.
解:设![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
∴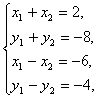 解得
解得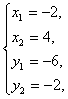 即
即![]() ,
,![]() .
.
于是![]()
![]() 且
且![]() ,
,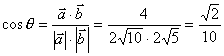 .
.
小结:设计本题的意图是将向量加减法的坐标形式与本节知识结合.
例3.已知两个非零向量![]() 和
和![]() 满足
满足![]() ,求证:
,求证:![]() .
.
分析:将已知条件代数化,通过代数变换得到代数结论,再将代数结论几何化.
证明:设![]() ,
,![]() ,
,
则![]() ,
,
![]() .
.
![]()
![]() ,
,
∴![]()
![]() ,
,
化简得![]() ,即
,即![]() .
.![]()
小结:本题运用向量的坐标形式来解决垂直问题,其实并不一定非用这个方法,而且这个方法还不是最简单的,只是通过本题使学生熟悉这种证明方法.
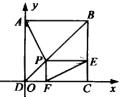 例4.如图所示,四边形ADCB是正方形,P是对角线DB上的一点,PFCE是矩形。试用向量法证明:
例4.如图所示,四边形ADCB是正方形,P是对角线DB上的一点,PFCE是矩形。试用向量法证明:
(1)![]() ;(2)
;(2)![]() 。
。
分析:如果我们能用坐标来表示![]() 与
与![]() ,则要证明的两结论,只要分别用两点间的距离公式和两向量垂直的充要条件进行验证即可。因此只要建立适当的坐标系,得到点A、B、E、F的坐标后,就可进行论证。
,则要证明的两结论,只要分别用两点间的距离公式和两向量垂直的充要条件进行验证即可。因此只要建立适当的坐标系,得到点A、B、E、F的坐标后,就可进行论证。
证明:以点D为坐标原点,DC所在直线为x轴建立如图所示的坐标系,设正方形的边长为l。
![]() ,则
,则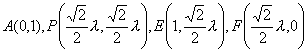 。
。
于是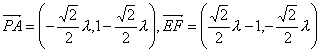 。
。
(1)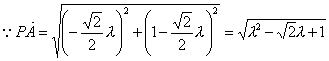 ,
,
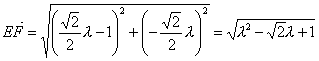 ,
,
∴![]() 。
。
(2)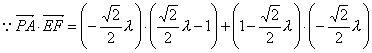
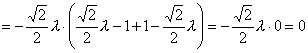 ,
,
∴![]() 。
。
小结:把几何图形放在适当的坐标系中,就赋予了有关点与向量具体的坐标,这样就能进行相应的代数运算和向量运算,从而使问题得到解决。这种解题方法具有普遍性,应该把它掌握好,其中坐标系的建立很重要,它关系到运算的简与繁。
例5. 已知:![]() 。
。
(1)求证:![]() 与
与![]() 互相垂直;
互相垂直;
(2)若![]() 与
与![]() 大小相等,求
大小相等,求![]() (其中
(其中![]() 且
且![]() )。
)。
分析:利用向量垂直的充要条件及向量模的公式解题。
解:(1)依题意知
![]() ,
,
![]() ,
,
又![]()
![]()
![]()
所以![]() 。
。
(2)由于 ![]() ,
,
所以 ![]() 。
。
又因为 ![]() ,所以
,所以
![]() ,且
,且![]() ,故
,故 ![]() 。又
。又![]() ,所以
,所以 ![]() 。
。
小结:对于(1)还有另解:由于![]()
![]()
![]()
![]()
![]()
![]() ,所以
,所以![]() ;对于(2)也有另解:由
;对于(2)也有另解:由![]() 得
得![]() ,进一步有
,进一步有![]() ,由此可得
,由此可得 ![]() .
.