第五节 线段的定比分点

典型例题

　　例1．已知 ， ，且 ， ，求点 、 的坐标.

　　分析：借助线段的定比分点式求解.

　　解：设 ， .

　　由 ，可得 ，即 ， .

　　运用定比点公式可知

　　 

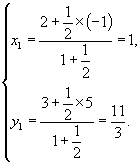
　　仿上可求得  ，

　　综上可知，欲求 、 两点坐标为 ， .

　　小结：对于本题欲求 点的坐标时，也可以由 ，得到 ，从而由定比公点公有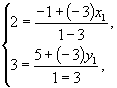 得 ， . 同理，也可以由 求得 点坐标，这表明，我们在利用定点比分点公式时，既要注意使用公式的前提，同时也要注意灵活地使用公式。

　　例2．已知 的三顶点坐标分别为 ， ， ，直线 ，交 于 ，且直线 平分 的面积，求 点坐标.

　　分析：本题是平面几何知识与定点分点公式的综合应用题，解题时，应先确定 分 的比，再利用公式求解.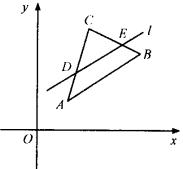

　　解：设直线交 于 ，依题意， ，又因为 ，故 ∽ ，所以 ， . 即点 分 的比为 .

　　设 的坐标为 ，由定比分点公式有 ， .

　　∴ 点的坐标为 .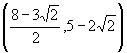

　　小结：求解定比分点坐标的关键是求出定比 的值. 求 的值，除注意 的符号外，还常常用到平面几何知识，如相似形的性质，比例线段等等。

　　例3．已知 、 不共线， ， ，将符号下列条件的 向量写成 的形式：

　　（1）点 分 所成的比 ，求 ；

　　（2）点 分 所成的比 ，求 .

　　分析：借助定比分点的概念解题。

　　解：（1）由 ，得 ，

　　即 .

　　故 ，

　　即 .

　　（2）由上可知

　　即  .

　　小结：本题从表面上看不涉及分点的坐标问题，但利用定比分点的概念，导出了 这个与定比 有关的等式，这实际上是定比分点坐标公式的另一种表现形式，即向量形式. 值得注意的是，这个等式在解决与向量有关的一些数学问题时很有用处。

　　例4．若直线 与连接 、 两点的线段有交点，求实数 的取值范围．

　　分析：当直线与线段 有交点时，这个交点分有向线段 所成的比 不小于0，从而得到关于 的不等式，但应注意考虑端点的情况．

　　解：当直线过 点时，有 ，∴ .

　　　　当直线过 点时，有 ，∴ .

　　　　当直线与线段 的交点在 、 之间时，设这个交点 分 的比为 ，它的坐标为 ，则

， .

　　而直线过 点，则 ，

　　整理，得 .

　　由 ，得 ，解得 或 .

　　故所求实数 的取值范围为 或 。

　　小结： (1)定比 的符号是求解本题的关键．应当注意，当点 在线段 上时， ；当点 在线段 或 的延长线上时， . 切不可将之混为一谈．

　　（2）恰当地利用定比 的几何意义，可以解决某些看似与定比分点坐标公式无关的数学问题．

返回页首