第四节 平面向量的坐标运算

典型例题

　　例1．设向量 ， ， ，则“ ∥ ”是“ ”的

　　（A）充分不必要条件                 （B）必要不充分条件

　　（C）充要条件                       （D）既不充分也不必要条件

　　分析：根据向量的坐标运算和充要条件的意义进行演算即可．

　　解：若 ∥ ，∵ ，则 ，代入坐标得： ，即 且 _．

消去r，得

　　反之，若 ，则 且

　　即

　　则 ，

　　∴ ∥

　　∴“ ∥ ”是“ ”的充要条件．

　　答案C．

　　小结：本题意在巩固向量平行的坐标表示．

　　例2．已知 =（1，-1）， =（-1，3）， =（3，5），求实数x、y，使 =x +y ．

　　分析：根据向量坐标运算和待定系数法，用方程思想求解即可．

　　解：由题意有

　　x +y =x（1，-1）+y（-1，3）=（x-y，-x+3y）．

　　又 =（3，5）

　　∴　x-y=3且-x+3y=5

　　解之得 x=7 且y=4

　　小结：在向量的坐标运算中经常要用到解方程的方法．

　　例3．已知A（-1，2），B（2，8）， = ， =- ，求点C、D和向量 的坐标．

　　分析：待定系数法设定点C、D的坐标，再根据向量 ， 和 关系进行坐标运算，用方程思想解之．

　　解：设C、D的坐标为（ ）、（ ），由题意得

　　 =（ ）， =（3，6）

　　 =（ ）， = （-3，-6）

　　又 = ， =-

　　∴（x₁+1，y₁-2）= （3，6）， （-1-x₂，2-y₂）=- （-3，-6）

　　即 ，

　　∴ 且 ， 且

　　∴ 且 ， 且

　　∴点C、D和向量 的坐标分别为（0，4）、（-2，0）和（-2，-4）

　　小结：本题涉及到方程思想，对学生运算能力要求较高．

　　例4．已知任意四边形ABCD中，E、F分别是AD、BC的中点，如图1，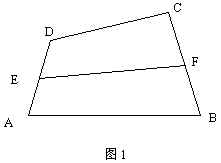

　　求证： = （ + ）．

　　证法一：

　　∵E、F分别是AD、BC的中点

　　∴ + = + =

　　又 = + +

　　　 = + +

　　两式相加得

　　2 = +

　　即 = （ + ）．

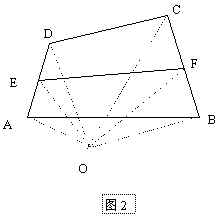
　　证法二：在平面内任取一点Ｏ（如图2），

　　∵E、F分别是AD、BC的中点

　　∴ = （ + ）

　　　 = （ + ）

　　∴ = -

　　　　　= [（ - ）+（ - ）]= （ + ）

　　∴ = （ + ）．

　　证法三：建立直角坐标系A（ ），B（ ），C（ ），D（ ）

　　则　 =（ ）， =（ ）

　　∴ （ + ）=（ ， ）

　　又　E（ ， ），F（ ， ）

　　则　 =（ - ， - ）

　　∴ = （ + ）．

　　小结：本题证法较多，利于开阔学生思路，同时三种证法各有千秋，证法二和证法三都是向量中常用方法，还有一定美感．

　　例5．已知向量 ，且 ，求 。

　　分析：分别求出向量u与v的坐标以后，再根据向量平行的坐标表示进行求解。

　　解法一：据已知可得

　　

　　由 ，知存在 ，使 ，即

　　

　　也即        解得    。

　　解法二：由解法一知，

　　∵ ，∴ ，得 。

　　小结：向量共线定理在向量解题中有较广泛地应用，但在具体应用中，使用其两种形式的哪一种，要视具体情况来决定。如在本例中，显然使用其坐标形式解题过程简捷一些。

返回页首