第三节 实数与向量的积

典型例题

例1．如图，已知向量 ， ， ，求作向量 .

　　分析：作向量的和差倍分问题，可以用三角形法则或平行四边法则。

　　作法一：用三角形法则，如图.

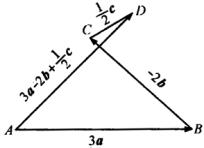
　　此时，由向量的加法可知，欲求作的向量为 .

　　作法二：利用平行四边形法则，如图

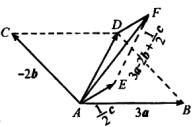
　　作 ， ， 。

　　分别以 的对角钱 以及 为邻边作 ，则向量 为所求作的向量．

　　小结：向量的加法、减法、实数与向量的积是向量中基本的运算，不仅要掌握其运算法则，更应理解这些运算的几何意义．另外，在求作本题时，若利用减法的几何意义作出 ，则更容易失误．所以在作向量的和差倍分时，一般可把“差”转换成“和”来作．

　　例2．已知向量a、b是两非零向量，在下列四个条件中，能使a、b共线的条件是（  ）

　　① 且 ；

　　②存在相异实数 、u，使 ；

　　③ （其中实数x、y满足 ；

　　④已知梯形ABCD中，其中 、 。

　　A．①②  B．①③  C．②  D．③④

　　分析：A、B均含有①，而C、D均含有④，所以可先判定①或④。若①能使a、b共线，则只有从A、B中进一步作出选择，若①不能使a、b共线，则应从C、D中进一步作出选择。首先判定①能否使a、b共线。由向量方程组： 可求得： ，∴a、b共线，因此可排除C、D。而由②可得 、u是相异实数，所以 、u不同时为0，不防设 ，故a、b共线，所以排除B，选择A。

　　答案：A

　　小结：条件③中当 时，就不能得到a、b共线。其实，在条件③中若添上 ，则不仅可得a、b共线，而且可得 。

　　条件④中没有明确AB、CD是上、下底，因此它们也可能是两腰，故条件④不能得到a、b共线。

　　例3．如图， 是一个梯形， 且 ， 、 分别是 和 的中点，已知 ， ，试用 ， 表示 和 .

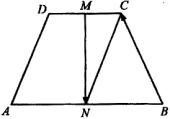
　　分析：利用三角形法则（平行四边形法则）求解，也可利用“首尾顺次相接的问量构成封闭图形时，其中各向量的和为0”解题．

　　解法一：连结 ， 是 的中点，∵ ，∴四边形 是平行四边形， .

　　又∵ ∴ ，

　　∴

　　解法二：在梯形 中，有 ，即 ，得 .

　　仿上，在四边形 中，利用 ，可得 .

　　小结：从解法二可以看出，利用前述这条向量的性质解题确实显得简捷．另外，本例本质上是平面向量基本定理的具体应用，因为 ， 是两个不共线的向量，所以 及 可以用它们来表示。

　　例4  如图，设 为 内一点， ，且 ， ， ， ，试求 ， .

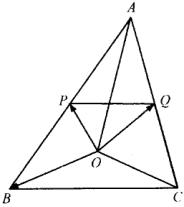　　　分析：根据题设，考虑用三角形法则求 ， ，即由 ， ，再利用平面几何及向量知识求出 ， 便可解决问题。

解：由平面几何知， ∽ ，且对应边之比为 ，

　　故  ，

　　又 、 、 与 、 、 分别共线，即知

　　 ， .

　　∴

　　即 

　　

　　即 

　　小结：利用三角形法则求某一个向量时，选取第三个点时，应注意恰当性，如本题中，若采用 ， ，虽然也可求出 ， 来，但计算过程就显得复杂些。

　　例5．设两非零向量 和 不共线，

　　（1）如果 ， ， ，求证 ， ， 三点共线.

　　（2）试确定实数 ，使 和 共线。

　　分析：要证明 ， ， 三点共线，须证存在 使 即可 。而若 与 共线，则一定存在 ，使 .

　　（1）证明  ∵ ， ，

　　∴ ， 共线，又有公共点

　　∴ ， ， 三点共线.

　　（2）解  ∵ 与 共线，

　　∴存在 使 ，

　　则 ，由于 与 不共线，

　　只能有 则 .

　　小结：本题充分地运用了向量共线的充要条件，即 与 共线 存在 使 （正用与逆用）