 设为首页
设为首页
 加入收藏
加入收藏
例1.如图1所示,已知向量![]() ,试求作和向量
,试求作和向量![]() .
.
分析:求作三个向量的和的问题,首先求作其中任两个向量的和,因为这两个向量的和仍为一个向量,然后再求这个向量与另一个向量的和.即先作![]() ,再作
,再作![]() .
.
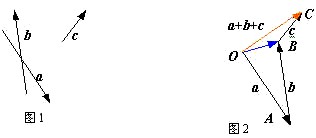
解:如图2所示,首先在平面内任取一点![]() ,作向量
,作向量![]() ,再作向量
,再作向量![]()
![]() ,则得向量
,则得向量![]() ,然后作向量
,然后作向量![]() ,则向量
,则向量![]() 即为所求.
即为所求.
小结:此题的目的主要在于用几何作图熟悉加法的三角形法则及对结合律的认识.
例2.化简下列各式
(1)![]() ; (2)
; (2)![]() .
.
分析:化简含有向量的关系式一般有两种方法①是利用几何方法通过作图实现化简;②是利用代数方法通过向量加法的交换律,使各向量“首尾相连”,通过向量加法的结合律调整向量相加的顺序,有时也需将一个向量拆分成两个或多个向量.
解: (1)原式=![]()
(2)原式=![]() .
.
小结:向量的加法,减法的运算并不困难,但运算的途径很多,十分灵活,如平面任一向量都可以写成两个向量的和,同样任一向量都可以分成两个向量的差等.通过这种调整来简化运算.
例3.用向量方法证明:对角线互相平分的四边形是平行四边形.
分析:要证明四边形是平行四边形只要证明某一组对边平行且相等.由相等向量的意义可知,只需证明其一组对边对应的向量是相等向量.(需首先将命题改造为数学符号语言)
已知:如图3,ABCD是四边形,对角线AC与BD交于O,且AO=OC,DO=OB.
求证:四边形ABCD是平行四边形.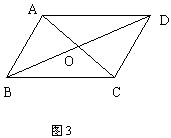
证明:由已知得![]() ,
,
![]() ,且A,D,B,C不在同一直线上,
,且A,D,B,C不在同一直线上,
故四边形ABCD是平行四边形.
小结:这种类型的题目由于要求用向量的方法来证明,故应把平面几何的语言准确无误的转换为平面向量的语言,如本题中![]() ∥
∥![]()
![]() ,而不能写
,而不能写![]() ∥
∥![]()
![]() .
.
例4.证明:对于任意两个向量![]() 都有
都有![]() .
.
分析:由于不等式本身有明显的几何意义,故应选用向量的几何意义进行证明.可根据向量![]() 共线与不共线两种情况进行讨论.
共线与不共线两种情况进行讨论.
证明:若![]() 中有一个为零向量,则不等式显然成立.若
中有一个为零向量,则不等式显然成立.若![]() 都不是0时,记
都不是0时,记![]() ,则
,则![]() .
.
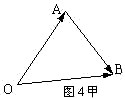
(1) 当![]() 不共线时,如图4甲所示,则有
不共线时,如图4甲所示,则有![]() .即
.即![]() .
.
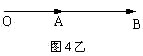
(2) 当![]() 共线时,若
共线时,若![]() 同向,如图4乙所示,
同向,如图4乙所示,![]() ,即
,即![]() ;
;
若![]() 反向,如图4丙所示
反向,如图4丙所示![]() ,即
,即![]() .
.
综上可知![]() .
.
小结:两个向量之间无大小可言而两个向量的长度之间可以比大小.此不等式一般称为三角不等式,它的几何意义就是三角形中的任意一边的长小于其他两边长的和且大于其他两边长的差的绝对值.在证明之后还可以让学生一起讨论不等式中两个等号成立的条件.
例5.设a表示“向东走10km”,b表示“向西走5km”,c表示“向北走10km”,d表示“向南走5km“.说明下列向量的意义.
(1)a+b (2)b+d (3)d+a+d
分析:根据实际意义来确定向量的方向,再根据三角形法则进行加法运算.
解:(1) a+b表示向东走5km.
(2) b+d表示向西南走![]() km
km
(3) d+a+d表示向东南走![]() km.
km.
小结:关于向量的加法实际就是向量的合成,而向量的合成在实际中有着广泛的应用,此题就是初步了解其应用.
例6.如图5,一物体受到两个大小均为60N的力的作用,两力的夹角为60![]() 且有一力方向水平,求合力的大小及方向.
且有一力方向水平,求合力的大小及方向.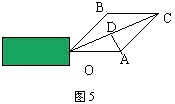
分析:首先应根据题目已知条件作出向量图,从图中观察合力与分力的关系.
解:设![]() 分别表示两力,以
分别表示两力,以![]() 为邻边作平行四边形OACB,则
为邻边作平行四边形OACB,则![]() 即为合力.
即为合力.
由已知可得△OAC为等腰三角形,且![]() .过A作
.过A作![]() 于
于![]() ,则在
,则在
![]() 中,
中,![]() .
.
故![]() ,即合力的大小为
,即合力的大小为![]() ,方向与水平方向成30°角.
,方向与水平方向成30°角.
小结:在这种向量的合成中注意和向量的模并不是两向量的模的简单相加,只有在两向量方向相同时才可以.