第一节 向量

典型例题

　　例1．判断下列命题的真假：

　　①直角坐标系中坐标轴的非负轴都是向量；

　　②两个向量平行是两个向量相等的必要条件；

　　③向量 与 是共线向量，则 、 、 、 必在同一直线上；

　　④向量 与向量 平行，则 与 的方向相同或相反；

　　⑤四边形 是平行四边形的充要条件是 ．

　　分析：判断上述五个命题的真假性，需细心辨别才能识其真面目．

　　解：①直角坐标系中坐标轴的非负半轴，虽有方向之别，但无大小之分，故命题是错误的．

　　②由于两个向量相等，必知这两个向量的方向与长度均一致，故这两个向量一定平行，所以，此命题正确；

　　③不正确．∵ 与 共线，可以有 与 平行；

　　④不正确．如果其中有一个是零向量，则其方向就不确定；

　　⑤正确．此命题相当于平面几何中的命题：四边形 是平行四边形的充要条件是有一组对边平行且相等．

　　小结：学习向量时，由于向量具有数形两重性，所以不仅要知其本身的一些概念性质，还应与相关的平面几何知识联系起来，这对理解向量的一些性质很有好处．

　　例2．下列各量中是向量的有_______________.

　　A   动能   B 重量  C  质量   D  长度  E  作用力与反作用力   F  温度

　　分析：用向量的两个基本要素作为判断的依据注意对物理量实际意义的认识.

　　解:A，C，D，F只有大小，没有方向，而B和F既有大小又有方向，故为向量.

　　小结：:此题意在加强应用意识，注重与其他学科的综合，在应用背景中认识大小和方向的含义，强化对向量的认识．

　　例3．命题“若 ， ，则 ．”（      ）

　　A．总成立　　B．当 时成立　　C．当 时成立　　D．当 时成立

　　分析：这里要作出正确选择，就是要探求题中命题成立的条件．∵零向量与其他任何非零向量都平行，∴当两非零向量 、 不平行而 时，有 ， ，但这时命题不成立，故不能选择A，也不能选择B与D，故只能选择C．

　　答案：C

　　小结：本例说明向量平行的传递性要成立，就需“过渡”向量 不为零向量．事实上，在 的情况下：① 时，∵ ，∴ 与 同向或反向．又∵ ，∴ 与 同向或反向，∴ 与 同向或反向，∴ ．②若 与 中有一个为零，则另一个无论为零还是不为零，均有 ．由以上①②可以确定 是正确的．

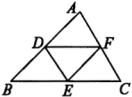　　 例4．如图， 、 、 分别是△ 的三边 、 、 的中点，写出与 共线的向量．

　　分析：要注意到线段 是△ 的中位线，与 共线的向量的主要特性是与 平行，结合中位线的性质可以得出结论．

　　解：与 共线的向量有 、 、 、 、 、 、 ．

　　小结：应注意共线向量就是平行向量，所以在图中凡是与 共线或平行的有向线段所表示的向量都是与 共线的向量．

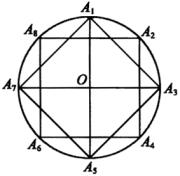　　 例5．如图， 、 … 是⊙ 上的八个等分点，则在以 、 … 及圆 九个点中任意两点为起点与终点的向量中，模等于半径的向量有多少？模等于半径 倍的向量有多少个？

　　分析：（1）由于 、 … 是⊙ 上的八个等分点，所以八边形 … 是正八边形，正八形的边及对角线长均与⊙ 的半径不相等．所以模等于半径的向量只可能是 与 （ 、2…8）两类．

　　（2）⊙ 内接正方形的边长是半径的 倍，所以我们应考虑与圆心 形成 圆心角的两点为端点的向量个数．

　　解：（1）模等于半径的向量只有两类，一类是 （ 、2…8）共8个；另一类是 （ 、2…8）也有8个．两类合计16个．

　　（2）以 、 … 为顶点的⊙ 的内接正方形有两个，一个是正方形 ；另一个是正方形 ．在题中所述的向量中，只有这两个正方形的边（看成有向线段，每一边对应两个向量）的长度为半径的 倍．所以模为半径 倍的向量共有 个．

　　小结：（1）在模等于半径的向量个数的计算中，要计算 与 （ 、2…8）两类．一般地我们易想到 （ 、2…8）这8个，而易遗漏 （ 、2…8）这8个．

　　（2）圆内接正方形的一边对应了长为 的两个向量，例如边 对应向量 与 ，因此与（1）一样，在解题过程中主要要防止漏算．认为满足条件的向量个数为8是错误的．

　　例6．在平面中下列各种情形中，将各向量的终点的集会分别构成什么图形？

　　（1）把所有单位向量的起点平移到同一点 ．

　　（2）把平行于直线 的所有单位向量的起点平移到直线 上的 点．

　　（3）把平行于直线 的所有向量的起点平移到直线 上的点 ．

　　解：（1）以点 为圆心，1为半径的圆．

　　　　（2）直线 上与点 的距离为1个长度单位的两个点．

　　　　（3）直线 ．

　　小结：本小题考查向量的平移变换和单位向量等基础知识，考查对向量与集合知识的综合运用能力．

返回页首