第十节 正切函数的图象和性质

典型例题

　　例1．比较下列各数大小：

　　（1） 与 ；（2） 与 ．

　　分析：同名函数比较大小时，应化为同一单调区间上两个角的函数值后，应用函数的单调性解决；而对于不同名函数，则应先化为同名函数再按上面方法求解．

　　解：（1）

　　因为 ，而 在 内是增函数

　　所以 ，    即

　　（2）

　　

　　而 在 内是增函数，所以

　　即  

　　小结：比较两个三角函数值的大小，首先将函数名称统一，再利用诱导公式将角转化到同一个单调区间内，通过函数的单调性进行比较大小．

　　例2．求函数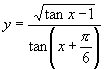 的定义域．

　　分析：根据自变量 满足的条例列出不等式组，解之即可．

　　解：由题得：

　　

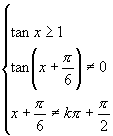
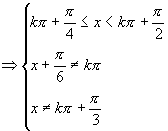
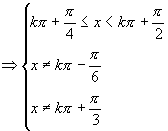
　　所以定义域为 （ ）．

　　小结：注意不要忽略了正切函数存在的条件，本题中是 ， ．

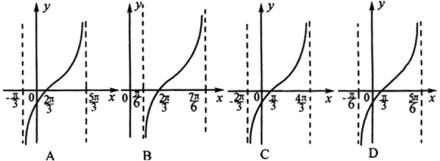
　　例3．（1）如图，函数 在一个周期内的图像是（     ）

　　

　　（2）要得到 的图像，只需将 的图像（      ）

　　A．向左平移 个单位　　B．向右平移 个单位

　　C．向左平移 个单位　　D．向右平移 个单位

　　分析：对于（1），可从周期、与 轴的交点等方面判断真假；对于（2），可将 化成 ，但要注意不是平移 的图像．

　　解：（1）由函数表达式 知，这个函数的最小正周期为 ，因此可排除 、 ，又函数表达式可化成 ，而这个函数的图像与函数 的图像形状相同，且将其向右侧平移 个单位．答案：A

　　（2）因为 ，所以将其向右平移 个单位可得 的图像．答案：D

　　小结：对于正切函数 （ ， ）的图像变换问题完全可比照正弦函数 （ ， ）的图像变换过程进行．

　　例4．作出函数 的图像，并根据图像求其单调区间．

　　分析：要作出函数 的图像，可先作出 的图像，然后将它在 轴上方的图像保留，而将其在 轴下方的图像向上翻（即作出关于 轴对称图像，）就可得到 的图像．

　　解：由于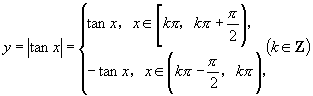

　　所以其图像如图所示，单调增区间为 ；单调减区间为 ．

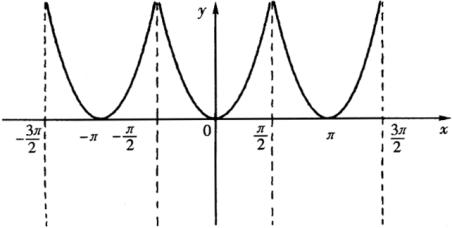
　　小结：利用正切函数的图象过 （0，0）三点且以 ， 为渐近线，这样根据这三点两线就可以大体勾画出此图．再利用图象变换得到题目要求的图象，推导出函数性质．

　　例5．求函数 的最小正周期．

　　分析：化简函数式半作出图形，再从图像上观察．

　　解：∵ （ ， ），作出 （ ， ）的图像．

　　小结：求函数的周期通常有两种方法：转化为已知函数和图象观察，通过图象观察要注意图象草图尽量准确，尤其是定义域的范围．

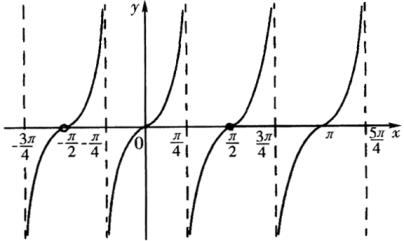
　　从图像上面可以看出函数 的最小正周期为 ．

　　小结：在函数化简的过程中一定要注意函数的等价变换，尤其是要注意定义域．

返回页首