 设为首页
设为首页
 加入收藏
加入收藏
例1.(l)利用“五点法”作函数![]() 的图象,并指出这个函数的振幅、周期和初相.
的图象,并指出这个函数的振幅、周期和初相.
(2)怎样由![]() 的图象得到
的图象得到![]() 的图象?
的图象?
解:(1)列表:
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
0 |
2 |
0 |
-2 |
0 |
描点:(![]() ,0),(
,0),(![]() ,2),(
,2),(![]() ,0),(
,0),(![]() ,-2),(
,-2),(![]() ,0)。
,0)。
用光滑的曲线将它们连结起来,就得到函数![]() 在一个周期内的简图(图1).把这个简图利用函数的周期性向左、右扩展,就得到函数
在一个周期内的简图(图1).把这个简图利用函数的周期性向左、右扩展,就得到函数![]() 的简图.
的简图.
振幅![]() ,周期
,周期![]() ,初相
,初相![]()
(2)解法一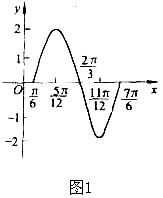
①把函数![]() 的图象上所有点向右平移
的图象上所有点向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象;②把函数
的图象;②把函数![]() 图象上所有点的根坐标缩短到原来的
图象上所有点的根坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象;③把函数
的图象;③把函数![]() 图象上所有的点的纵坐标伸长到原来的2倍(横坐标不变),就得到函数
图象上所有的点的纵坐标伸长到原来的2倍(横坐标不变),就得到函数![]() 的图象见图1.
的图象见图1.
解法二
①把函数![]() 的图象上所有的点的横坐标缩短到原来的
的图象上所有的点的横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象;②把函数
的图象;②把函数![]() 图象上所有的点向右平移
图象上所有的点向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象;③把函数
的图象;③把函数![]() 的图象上所有的点的纵坐标伸长到原来的2倍(根坐标不变),就得到函数
的图象上所有的点的纵坐标伸长到原来的2倍(根坐标不变),就得到函数![]() 的图象见图1.
的图象见图1.
例2.已知函数![]() 在一个周期内的简图(如图)。求其相应的函数表达式,并说明它是
在一个周期内的简图(如图)。求其相应的函数表达式,并说明它是![]() 经过怎样变换得到的。
经过怎样变换得到的。
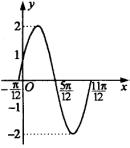 分析:应求出A、
分析:应求出A、![]() 、
、![]() ,观察图像易知振幅
,观察图像易知振幅![]() ,周期
,周期![]() ,从而求得
,从而求得![]() ,对于
,对于![]() ,只需将点
,只需将点![]() 代入解析式即可通过解方程获得。得知函数表达式则图像变换易知。
代入解析式即可通过解方程获得。得知函数表达式则图像变换易知。
解:因为![]() ,所以
,所以![]() ,又易知
,又易知![]() ,所以
,所以![]() 。将点
。将点![]() 代入上式得
代入上式得![]() 。即
。即![]() ,由
,由![]() 得
得![]() ,所以
,所以![]() 。
。
它的图像可由![]() 的图像作如下变换得到:
的图像作如下变换得到:

小结:利用图像特征确定函数解析式![]() 或根据代数条件确定解析式时,要注意以下几种常用方法:
或根据代数条件确定解析式时,要注意以下几种常用方法:
(1)振幅![]() .
.
(2)相邻两个最值对应的横坐标之差,或者一个单调区间的长度为![]() ,由此推出
,由此推出![]() 值.
值.
(3)确定![]() 值,一般用给定特殊点坐标代入解析式来确定.
值,一般用给定特殊点坐标代入解析式来确定.
例3. 函数![]() ,当它表示一个振动量时,求出它的振幅、周期、频率。相位、初相.
,当它表示一个振动量时,求出它的振幅、周期、频率。相位、初相.
解:振幅![]() ,周期
,周期![]() ,频率
,频率![]() ,相位是
,相位是![]() ,初相是
,初相是![]() 。
。
例4. 单摆从某点开始来回摆动,离开平衡位置的距离![]() (厘米)和时间
(厘米)和时间![]() (秒)的函数关系为
(秒)的函数关系为
(l)作出它的图像;
(2)单摆开始摆动(![]() )时,离开平衡位置多少厘米?
)时,离开平衡位置多少厘米?
(3)单摆摆动到最右边时,离开平衡位置多少厘米?
(4)单摆来回摆动一次需多少时间?
解:(l)找出曲线上的五个特殊点,列表如下:
|
|
… |
|
|
|
|
|
… |
|
|
… |
0 |
|
|
|
2 |
… |
|
|
… |
0 |
6 |
0 |
-6 |
0 |
… |
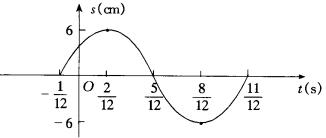
用光滑曲线连接这些点,得函数![]() 的图像(如图)
的图像(如图)
(2)当![]() 时,
时,![]() ,即单摆开始摆动时,离开平衡位置3
,即单摆开始摆动时,离开平衡位置3![]() 。
。
(3)![]() 的振幅为6,所以单摆摆动到最右边时,离开平衡位置6
的振幅为6,所以单摆摆动到最右边时,离开平衡位置6![]() 。
。
(4)![]() 的周期
的周期![]() ,所以单摆来回摆动一次需要的时间为1
,所以单摆来回摆动一次需要的时间为1![]() 。
。
评注:在作图时,如无特殊声明,一般用五点法作图较简便
例5.函数![]() 的横坐标伸长到原来的两倍,再向左平移
的横坐标伸长到原来的两倍,再向左平移![]() 个单位,所得到的曲线是
个单位,所得到的曲线是![]() 的图像,试求函数
的图像,试求函数![]() 的解析式.
的解析式.
分析:这个问题有两种解法,一是考虑以上变换的“逆变换”,即将以上变换倒过来,由![]() 变换到
变换到![]() ;二是代换法,即设
;二是代换法,即设![]() ,然后按题设中的变换分两步得:
,然后按题设中的变换分两步得:![]() ,它就是
,它就是![]() ,即可求得
,即可求得![]() 、
、![]() 、
、![]() 的值.
的值.
解:解法一:问题即是将![]() 的图像先向右平移
的图像先向右平移![]() 个单位,得到
个单位,得到![]() ;再将横坐标压缩到原来的
;再将横坐标压缩到原来的![]() ,得
,得![]() ,即
,即![]() .这就是所求函数
.这就是所求函数![]() 的解析式.
的解析式.
解法二:设![]() ,将它的横坐标伸长到原来的两倍得到
,将它的横坐标伸长到原来的两倍得到![]() ;再将其图像向左平移
;再将其图像向左平移![]() 个单位,得
个单位,得![]()
![]()
![]() .
.
∴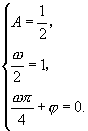 解之得:
解之得: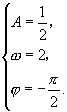
∴![]() ,即
,即![]() .
.
小结:以上两种解法各有“千秋”,均为求解类似问题的好方法,注意熟练掌握.
例6.已知函数![]() (
(![]() ,
,![]() ,
,![]() )的图像的一个最高点为(2,
)的图像的一个最高点为(2,![]() ),由这个最高点到相邻最低点,图像与
),由这个最高点到相邻最低点,图像与![]() 轴交于(6,0)点,试求这个函数的解析式.
轴交于(6,0)点,试求这个函数的解析式.
解 ∵最高点为(2,![]() ),
),
∴![]() ,由题意知从最高点到相邻最低点时交
,由题意知从最高点到相邻最低点时交![]() 轴于(6,0),
轴于(6,0),
∴![]() ,即
,即![]() .
.
∴![]() .
.
∴![]() 代入最高点坐标,
代入最高点坐标,
![]() ,
,
∴![]() ,
,
∴![]() .
.
∴函数解析式为![]()