 设为首页
设为首页
 加入收藏
加入收藏
【典例剖析】
例1 化简与求值.
(1) ![]()
(2) ![]()
分析:可先用诱导公式将三角式中的角度转化,然后再用两角和与差的三角公式化简与求值.
解:(1)原式 ![]()
![]()
![]()
![]()
(2)原式 ![]()
![]()
![]()
说明:本例第(1)题中四个角不相同,初看起来不能利用公式,但是当我们利用诱导公式将角度化为小于 ![]() 的正角后,就会发现其内在关系,而对于第(2)题中的
的正角后,就会发现其内在关系,而对于第(2)题中的 ![]() 与
与 ![]() ,由于它们互为补角,故也可用诱导公式化为相同的角.
,由于它们互为补角,故也可用诱导公式化为相同的角.
例2
求 ![]() 的值.
的值.
分析:发现此式与 ![]() 用和角正切公式展开后之间的内在联系,即可求得所求的值.
用和角正切公式展开后之间的内在联系,即可求得所求的值.
解:∵
![]()
去分母整理,得
![]()
说明:灵活运用公式体现在变形应用公式,如本例,和差角正切公式是分式形式,根据需要可化为整式.
3 已知 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
分析:由 ![]() 的范围及
的范围及 ![]() 的值,利用同角三角函数关系式可求
的值,利用同角三角函数关系式可求 ![]() 和
和 ![]() 的值,同理可求得
的值,同理可求得 ![]() 的值,再用已知角
的值,再用已知角 ![]() 及
及 ![]() 来表示未知角
来表示未知角 ![]() ,即
,即 ![]() ,然后利用两角差的余弦公式求得.
,然后利用两角差的余弦公式求得.
解:∵
![]() ,
, ![]()
∴
![]() .
.
∴
![]()
![]()
又∵ ![]() ,
, ![]()
∴ 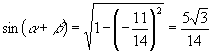
于是 ![]()
![]()
![]()
![]()
说明:本题获解的关键是将 ![]() 表示成:
表示成: ![]() .由于可以求
.由于可以求 ![]() 与
与 ![]() 相应三角函数值,所以利用两角差的余弦公式可顺利求得
相应三角函数值,所以利用两角差的余弦公式可顺利求得 ![]() 的值.
的值.
例4
已知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 与
与 ![]() .
.
分析:研究角与角的关系,发现 ![]() ,
,![]() ,再求余弦值.
,再求余弦值.
解:∵
![]() ,
, ![]() ,
,
∴
![]()
∵
![]() ,
, ![]() ,
,
∴
![]()
∴
![]()
![]()
![]()
![]()
![]()
![]()
例5
已知: ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
分析:欲求值,需化弦,得 ![]() ,可再求
,可再求 ![]() ,
, ![]()
解:∵
![]() ,∴
,∴
![]() ①
①
∵
![]() ,∴
,∴
![]() ②
②
(①+②)÷(①-②)
得 ![]()
说明:当题中异角、异名时,常需化角化名,有时将单角转化为复角(和或差),本题是利用展开,将复角化成单角,正(余)切和正(余)弦常常互化.
例6
已知: ![]() 是△
是△ ![]() 的三个内角,且
的三个内角,且 ![]() .试判断此三角形的形状特征.
.试判断此三角形的形状特征.
分析:(1)化去对数符号,对数式转化为有理式,(2)考察 ![]() 的关系及大小,据此判明形状特征.
的关系及大小,据此判明形状特征.
解:从 ![]() 可得
可得
![]() ,
, ![]() ,
,
![]()
![]() .
.
移项化为
![]()
即
![]() ∴
∴ ![]()
∴
△ ![]() 为等腰三角形.
为等腰三角形.
说明:(1)从角与角的关系探究三角函数间的关系;反之,利用三角函数间的关系去判断角的大小及关系,这是常用的基本方法.
(2)若此题用下面的方法继续探究下去,你认为怎样?为什么?
由于
![]() ∴
∴ ![]() 故
故 ![]() .
.
∵
![]() ∴
∴ ![]() ,
,
得 ![]() ,
, ![]() ,
, ![]() ,
,
∴ 此三角形是等腰直角三角形.
例7
在△ ![]() 中,求证
中,求证 ![]() .
.
分析:
注意到 ![]() ,∴
,∴ ![]() ,
,
移项得 ![]() ,取正切,用诱导公式和
,取正切,用诱导公式和 ![]() 整理即是.另外,
整理即是.另外, ![]() ,
, ![]()
![]() .都可得出相类拟的等式.
.都可得出相类拟的等式.
证明:
∵ ![]() ∴
∴ ![]()
故 ![]()
即
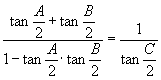
去分母得
![]()
例8
已知: ![]() 与
与 ![]() 是
是 ![]() 的解,若
的解,若![]() ,求
,求 ![]() 与
与 ![]() 的值.
的值.
分析:∵ ![]() 与
与 ![]() 是二个未知数,∴列出二个方程便可解得.
是二个未知数,∴列出二个方程便可解得.
解:设 ![]() ,则
,则 ![]() ,
,
∵
![]() ,∴
,∴
![]() ,
,
解得 ![]() 或
或 ![]() .
.
(Ⅰ)当 ![]() 时,有
时,有 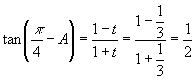 ,
,
∴
![]() ,
,
![]() .
.
(Ⅱ)当 ![]() 时,有
时,有 ![]() .
.
∴
![]()
![]() .
.
![]()
说明:“列方程求未知数”这是数学的常用方法,要熟悉方程的思想方法并会灵活运用,如果 ![]() ,
, ![]() 是某二次方程的二根,则韦达定理与公式
是某二次方程的二根,则韦达定理与公式 ![]() 有着必然的联系;若
有着必然的联系;若 ![]() ,
, ![]() 是某二次方程的二根,则韦达定理与
是某二次方程的二根,则韦达定理与 ![]() 有着必然联系,要充分利用这些联系解题.
有着必然联系,要充分利用这些联系解题.