 设为首页
设为首页
 加入收藏
加入收藏
例1 已知 ![]() ,试用
,试用 ![]() 表示其他五种三角函数.
表示其他五种三角函数.
分析:本题首先应注意对 ![]() 进行分类,再利用同角三角函数的关系求之.
进行分类,再利用同角三角函数的关系求之.
解:由于 ![]() ,且
,且 ![]() ,所以其他五种三角函数都有意义.
,所以其他五种三角函数都有意义.
(1)当 ![]() 在第一、二象限时,
在第一、二象限时,
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
(2)当 ![]() 在第三、四象限时,
在第三、四象限时,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
说明:解决此类问题时,应注意尽可能地确定 ![]() 所在的象限,以便确定三角函数的符号.另外,在用一个角的三角函数值表示其他几个三角函数值时,应尽可能少地使用平方关系.
所在的象限,以便确定三角函数的符号.另外,在用一个角的三角函数值表示其他几个三角函数值时,应尽可能少地使用平方关系.
例2 已知 ![]() ,求
,求 ![]() 的值.
的值.
分析:本题的解题思路入口处较宽,下面给出一种化切为弦的求法.
解:将已知等式两边平方得 ![]() .
.
由于 ![]() ,所以
,所以 ![]() ,
, ![]() ,从而
,从而 ![]() ,故
,故![]()
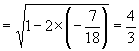 .
.
解方程组 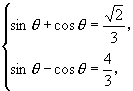 解得
解得 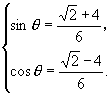
故 ![]() .
.
说明:对于本题还可以有其他多种解法,有兴趣的读者不妨一试,但值得注意的是,对本题如若解题时不很细主,则很容易发生误解,如以下这种解法:
由![]() .
.
即 ![]() ,解得
,解得 ![]() 或
或 ![]() .
.
你能看出其中的错误吗?
例3 化简 ![]() .
.
分析:对本题一般可采取化切为弦的办法进行化简.
解:原式 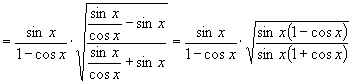
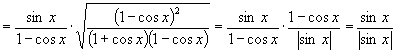
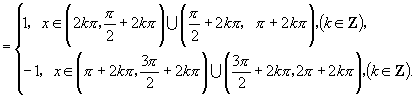
说明:化简三角函数式所得的最后结果,应满足以下要求:①函数的种类要最少;②项数要最少;③函数次数要最低;④能求出数值的要求出数值;⑤尽量使分母不含三角函数;⑥尽量使分母不含根式.
例4 求证 ![]() .
.
分析:对本题,可多角度地探究其证法.
证法一:左边 ![]()
![]()
![]() 右边.
右边.
证法二:右边-左边 ![]()
![]()
![]()
证法三:命 ![]() ,
, ![]() ,消
,消 ![]() 得
得 ![]() ,即
,即 ![]() ,
,
左边 ![]() 右边.
右边.
证法四:构造关于 ![]() 的方程
的方程 ![]() ,即
,即 ![]() ,解之得
,解之得 ![]() ,将其一根
,将其一根 ![]() 代入第一个方程,即有
代入第一个方程,即有
![]() .
.
说明:在本题的上述四种不同的证法当中,均体现了一种转化与化归的数学思想方法.