 设为首页
设为首页
 加入收藏
加入收藏
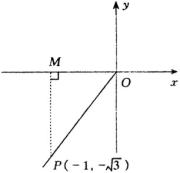
例1 若角 ![]() 的终边经过点
的终边经过点 ![]() ,试求
,试求 ![]() 的六个三角函数值和角
的六个三角函数值和角 ![]() 的集合
的集合 ![]() ,并求出集合
,并求出集合 ![]() 中绝对值最小的角.如图所示.
中绝对值最小的角.如图所示.
分析:应先找出 ![]() 的值.
的值.
解:∵ ![]() ,
, ![]() ,
,
∴ ![]() .
.
则
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
又∵ ![]() ,
,
∴ ![]() .
.
![]() .
.
故 ![]() 中绝对值最小的角是
中绝对值最小的角是 ![]() .
.
说明:此例是典型的考查定义的题.
例2 已知角 ![]() 的终边上一点
的终边上一点 ![]() ,(
,( ![]() )求角
)求角 ![]() 的六个三角函数值.
的六个三角函数值.
分析:与上例一样,应先求出 ![]() 及
及 ![]() .
.
解:∵ ![]()
![]() ,
,
则 ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
说明:此类题目应用定义解,但若此类题目没有给出 ![]() 的取值范围,要分类讨论求解.
的取值范围,要分类讨论求解.
例3 当 ![]() 为第二象限角,试求
为第二象限角,试求 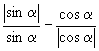 的值.
的值.
分析:应先由 ![]() 为第二象限角这一条件求出绝对值再求值.
为第二象限角这一条件求出绝对值再求值.
解:当 ![]() 为第二象限角时,
为第二象限角时, ![]() ,
, ![]() ,
,
故 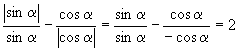 .
.
说明:此类题目旨在考查对符号的判定.
例4 若 ![]() ,且
,且 ![]() ,试确定
,试确定 ![]() 所在的象限.
所在的象限.
分析:用不等式表示出 ![]() ,进而求解.
,进而求解.
解:∵ ![]() ,∴
,∴ ![]() 在第一或第二象限,即
在第一或第二象限,即
![]() .
.
则 ![]() .
.
当 ![]() ,有
,有
![]() .
.
当 ![]() ,有
,有
![]() .
.
故 ![]() 为第一或第三象限.
为第一或第三象限.
又由 ![]() ,可知
,可知 ![]() 在第二或第三象限.
在第二或第三象限.
综上所述, ![]() 在第三象限.
在第三象限.
说明:应注意在求此题的最终解答时,要找出 ![]() 所在有关集合的交集.
所在有关集合的交集.
例5 计算:
(1) ![]() ;
;
(2) ![]() .
.
分析:应利用课本中给出的公式以及由此推得的下列公式化简求值.
![]() ;
;
![]() ;
;
![]() .
.
解:(1)原式
![]()
![]()
![]() .
.
(2)原式 ![]()
![]()
![]() .
.
说明:应对特殊角的三角函数值熟练掌握,以便准确应用.
例6 已知 ![]() 为锐角,试证:
为锐角,试证: ![]() .
.
分析:应在角 ![]() 的终边上任取一点,应用三角函数的定义来解之.
的终边上任取一点,应用三角函数的定义来解之.
证明:在角 ![]() 的终边上任取一点
的终边上任取一点 ![]() (异于原点),则
(异于原点),则
![]() ,
, ![]() .
.
∵ ![]() 为锐角,∴
为锐角,∴ ![]() ,
, ![]() .
.
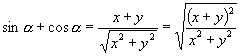
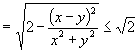 ,
,
又 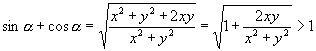 .
.
故 ![]() .
.
说明:(1)本例中,运用三角函数的定义,将三角函数表示为比例,从而将三角问题转化为代数问题而获解,这是一种十分重要的解题方法,应引起重视.
(2)本例中,应用了 ![]() ,
, ![]() .这种基本的不等关系应熟悉.
.这种基本的不等关系应熟悉.