第二节 弧度制

典型例题

例1  将下列各角化成 ，且 的形式，并指出它们是第几象限角：（1） ；（2） ．

分析  先把 化成 的形式，再用弧度制表示．

解（1）∵ ，

　　∴ 与 角的终边相同，又∵ 是第一象限角，

　　∴ 是第一象限角．

（2）∵ ，∴ 与 角的终边相同．

　　又∵ 是第三象限角，∴ 是第三象限角．

　　说明  用弧度制表示终边相同角 时， 是 的偶数倍，而不是整数倍．同时， 为弧度，不能写成 的形式．

例2  若弧度为2的圆心角所对的弦长为2，则这个圆心角所夹扇形的面积是（      ）

　　A． B． C． D．

分析  由扇形的面积公式 知，要求扇形的面积，只需求出扇形的半径 即可．

　　解  如图，过点 作 于 ，延长 ，交 于 ，则

　　 ＝ ＝ ，且 ．

　　在 中， ．

　　∴扇形的面积 ．

故选C．

例3  集合 ， ，则有（      ）．

　　A．B． C． D．

　　分析  对集合 中的整数 依次取0，1，2，3，得角 ， ， ， ， ， ， 角的终边相同．故选 ．

例4　　如图，用弧度制表示下列终边落在阴影部分的角的集合（不包括边界）．

　　

解（1）按逆时针方向，在区间 上与角 终边相同的角为 ，故所求集合为： ．

　　（2）图中第三象限部分可看成是由第一象限的阴影部分绕原点旋转 弧度而成的，故所求集合可表示为： ．

　　说明  当两区域的边界互为反向延长线时，只用一个式“ ”就可以表示．

　　（3）所求集合为： ．

例5  已知两角的和为1弧度，且两角的差为 ，求这两个角各是多少弧度．

　　分析  设两角的弧度数分别是 、 ，通过列方程组，就可以求出 、 ，但要注意单位的统一．

　　解  设两角的弧度数分别是 、 ，因为 ，

　　则依题意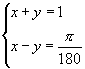，得 ，解之得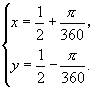

　　即所求两角的弧度数分别为 ， ．

返回页首