第一节 角的概念的推广

典型例题

　　例1  设 ， ， ， ，那么有（     ）．

　　A． 　　　　B．

　　C． （ ）　　D．

　　分析：解答本题时，先应明确所给集合中角的具体含义，再逐一对照每一个选项，明辨真伪．

　　解：第一象限的角不一定小于 （如 ），故A错；小于 的角不一定在第一象限（如 ），故B错； 的角 ，但 的角 ，故C错；又 ，因此D对，应选D．

　　说明：角的概念推广后，遇到角的问题，应根据角的范围及相关角的概念进行具体分析．如本题中的“锐角”与“小于 的角”就是两个含义不尽相同的概念．

　　例2  在 ～ 间，求出与下列各角终边相同的角，并判定它们分别是哪一个象限的角．

　　（1） ；　　（2） ．

　　分析：求解本题，其关键在于正确得到 中的 值，即用给出的角去除以 所得到的整数部分．

　　解：（1）因为 ，

　　所以  即为欲求的角，它在第三象限，从而 也是第三象限的角．

　　（2）因为 ，

　　所以 即为所求的角，它是第三象限的角，故 也是第三象限的角．

　　说明：在 ～ 内求终边与给定的角的终边相同的角时，若题中给定的角是负角，在应用式子 表示时， 比正常除法所得整数应小一个单位，才能使余数在 ～ 内，故这里的 只能取－2，而不能－1，若取－1，则 ，这种形式对解本题并无作用，因为 不在 ～ 之间．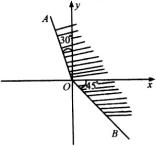

　　例3  （1）如图，终边落在 位置时的角的集合是____________；线边落在 位置，且在 内的角的集合是_________；终边落在阴影部分（含边界）的角的集合是______________．

　

　（2）已知 ，

　　　　　

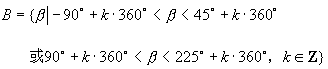
　　求 与 ．

　　分析：本题可借助数形结合的思想方法求解．

　　解：（1）由图形直观可得：终边落在 位置时角的集合是 ；终边落在 位置，且在 内的角的集合是 ；终边落在阴影部分（含边界）的角的集合是

．

　　（2）分别在直角坐标平面上画出表示集合 、 的示意图（ 为横线部分， 为竖线部分）（如图）再由图形直观得出：





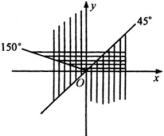
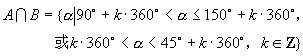
　　说明：求角值的集合的交集或并集时，借助数形结合是最简便的方法．

　　例4  已知 是第二象限的角，试求

　　（1） 角所在的象限；　　（2） 角所在的象限．

　　分析：对于本题，如若不进行较深入地推演，则很容易得到一个较明显而又错误的结论，即认为 角在第一象限； 角在第四象限，而事实上是不尽然的．

　　解：（1）因为 是第二象限的角，

　　所以 ，

　　从而有 ．

　　由上知，当 为偶数时， 角是第一象限的角；当 为奇数时， 角是第三象限的角．

　　综上可知， 角是第一或第三象限的角．

　　（2）由（1）可知， 角的范围是 ．

　　故 角是第三象限，或第四象限，或是 轴负半轴上的角．

　　说明：依照（1）中的方法，可得到以下规律：当 分别是第一、二、三、四象限时， 则可能顺次是第一或三、一或三、二或四、二或四象限的角．仿此，还可进一步考虑 的情形，有兴趣的读者不妨一试；另外，应注意，在（2）中，不可把 角答成是第三象限或第四象限的角，因为终边在 轴负半轴上的角 （ ）也是它的一个解，而此角不属于任何象限．