 设为首页
设为首页
 加入收藏
加入收藏
例1.已知 ![]() 为各项均为正数的等比数列,公比
为各项均为正数的等比数列,公比 ![]() ,则( ).
,则( ).
(A)
![]()
(B)
![]()
(C) ![]()
(D) ![]() 与
与 ![]() 的大小关系不确定
的大小关系不确定
分析:比较两数大小用到作差比较法.
解:
![]() ,
,
![]() ,
,
![]()
![]() -
- ![]()
=
![]() =
= ![]() .
.
因为
![]() 为各项均为正数,所以
为各项均为正数,所以 ![]() .
.
当
![]() 时有
时有 ![]() ,
, ![]() ;
;
当
![]() 时有
时有![]() ,也有
,也有 ![]() ,所以对任意正数
,所以对任意正数 ![]() 都有
都有 ![]() ,即
,即 ![]() ,故选择
,故选择 ![]() .
.
说明:通过本题的探索,复习基本量的方法,同时复习比较法的基本思路与方法.
例2.已知三角形的三边长成等比数列,求此等比数列的公比的取值范围.
分析:由三个数构成三角形三条边的条件建立关于公差的不等式(组).
解:设该等比数列的公比为
![]() ,一条边长为
,一条边长为 ![]() ,则三条边长分别为
,则三条边长分别为 ![]() .所以有
.所以有 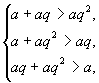 化简得
化简得 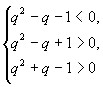

![]() ,
,
于是公比的取值范围是
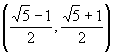 .
.
说明:本题是数列知识与几何知识、不等式的解法的综合题,正确解答的关键是把问题一步一步地转化.
例3.已知数列
![]() 是由正数构成的等比数列,公比
是由正数构成的等比数列,公比 ![]() ,且
,且 ![]() ,则
,则 ![]() 等于( ).
等于( ).
(A)![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
分析:利用等比数列相邻的三项之间的关系 ![]() ,使得变量减少.
,使得变量减少.
解:
![]()
![]()
![]() …,
…, ![]()
![]()
![]()
![]()
![]() …
… ![]() =
= ![]() ,
,
![]() .
.
![]()
![]() ,
,
![]() 选择(B).
选择(B).
说明:本题的一般解法是基本量法,即将所求各项均用 ![]() 表示,由已知的两个等式求出
表示,由已知的两个等式求出 ![]() ,代入所求即可,但运算量较大.本解法利用的是整体代换———通过观察发现项之间的关系,将30项平均分成了10组,寻求每组中的项之间的关系.本题还可求得
,代入所求即可,但运算量较大.本解法利用的是整体代换———通过观察发现项之间的关系,将30项平均分成了10组,寻求每组中的项之间的关系.本题还可求得
![]() .
.
例4. 有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和为16,第二个数与第三个数的和为12,求这四个数.
分析:解题思路是设未知数,列方程组,解方程组.
解:设这四个数依次为
![]() ,于是有
,于是有 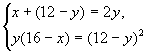 ,
,
解得
![]() 或
或 ![]() 故所求的四个数为0,4,8,16,或15,9,3,1.
故所求的四个数为0,4,8,16,或15,9,3,1.
说明:本题设未知数的方法很多,出所示解法外,还可设四个未知数,这样便须列四个方程.可能多数学生选择两个未知数,如利用等差数列这一条件,设四个数分别为 ![]() ,方程较为复杂,所以要选择适当的未知数,使得未知数尽量少,方程尽量简单.
,方程较为复杂,所以要选择适当的未知数,使得未知数尽量少,方程尽量简单.
例5.设二次方程
![]() 有两个实根
有两个实根 ![]() 和
和 ![]() ,且满足
,且满足 ![]() .
.
(1)试用
![]() 表示
表示 ![]() ;
;
(2)求证
![]() 是等比数列;
是等比数列;
(3)当
![]() 时,求数列
时,求数列 ![]() 的通项公式.
的通项公式.
分析:消去
![]() 得到
得到 ![]() ,
, ![]() 的关系,利用定义证明数列为等比数列.
的关系,利用定义证明数列为等比数列.
解:(1)由根与系数的关系得
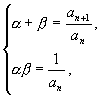 代入
代入 ![]() ,化简得
,化简得 ![]() .
.
证明:(2)因为
![]() ,所以
,所以 ![]() ,于是
,于是 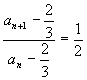 (可以证明
(可以证明 ![]() ),故
),故 ![]() 是公比为
是公比为 ![]() 的等比数列.
的等比数列.
解:(3)当
![]() 时,
时, ![]() ,所以
,所以 ![]() 是首项为
是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列.
的等比数列.
于是
![]() 故
故 ![]() .
.
说明:一些数列通过适当的变形,可以得到一个等比数列(或等差数列),形如 ![]() 的数列就可以转化为一个等比数列.
的数列就可以转化为一个等比数列.