第二节 等差数列

典型例题

　　例1.已知 依次成等差数列，求证： 依次成等差数列.

　　分析：要证三个数 成等差数列，只需证明等式： ，即证 成立.

　　证明： 成等差数列，

 （设其公差为 ），

，


　　又 ，

 ， 成等差数列.

　　说明：本题实质上是一个条件等式的证明，关键是条件如何使用.这种证法引入了一个新字母，使条件与结论中的字母减少，关系明朗.此题证法很多，不再一一列举.

　　例2 在等差数列 中， ，则 （       ）.

　　（A）72　　（B）60　　（C）48　　（D）36

　　分析：在题目中的项很多，利用通项公式转化为两个基本量 和 .

　　解：设此数列的首项为 ，公差为，则 ，即 .

　　说明：可以应用等差数列的性质：若 ，则，所以有 ＝ ＝40，故 60.

　　例3 已知是等差数列，且满足 ，则 等于________.

　　分析：已知等差数列的两项，等差数列便确定了，利用通项公式可以求得任意一项.数列确定后，数列的图像也确定了，利用图形也可求解.

　　解一：设此数列的首项为，公差为，则， ，

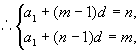相减得，

 ，_，

.

　　解二：设数列公差为 ，， .故 .

　　解三：根据等差数列的图像可知 三点共线，故有 ，即 ， .

　　说明： 通项公式与图像是认识和研究等差数列的工具，它们在数和形两个角度各有优势，应将它们有机结合，适当选择，以利问题解决.

　　例4.已知无穷等差数列 ，首项 公差 ，依次取出项数被4除余3的项组成数列 .

　　（1）求 和 ；

　　（2）求 的通项公式；

　　（3） 中的第110项是 的第几项？

　　分析：数列 是数列 的一个子数列，其项数构成以3为首项，4为公差的等差数列，由于 是等差数列，则 也是等差数列.

　　解：（1） ，

　　数列 中项数被4除余3的项是 的第3项，第7项，第11项，…，这些项组成一个新的等差数列（第二问中加以证明），其首项 ， .

　　（2）设 中的第 项是 的第 项，即 ，则 ，∴ 是等差数列，其通项公式为 .

　　（3） 设它是 中的第 项，则 ，则

　　说明：数列的项数相当于函数的自变量，通项公式相当于对应法则，对数列的研究应很好地把握项数，研究数列的子数列一定要研究二者项数的关系.

　　例5.设 是等差数列， ，且 ， .求等差数列的通项 .

　　分析：求 通项公式，关键是要确定数列的首项与公差.可设首项为 ，公差为 ，运用方程思想，列两个方程，解方程组即可.

　　解：设首项为 ，公差为 ，

　　由已知得

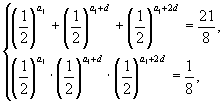
　　由第二个方程，化简为 解得 ，

　　所以 ，代入第一个方程得 即 化简得 解得 ，或 ，所以 或 ，故 或 .

　　说明：方程的思想是指把数学问题所反映的数量关系用解析式的形式表示出来，在把解析式归结为方程，通过解方程的手段或对方程进行研究使问题得以解决.设未知数，列方程，解方程是用方程的思想解数列问题的重要环节.

返回页首