 设为首页
设为首页
 加入收藏
加入收藏
例1.如图,一动点 ![]() 自边长为1的正方形
自边长为1的正方形 ![]() 的顶点
的顶点 ![]() 出发,沿正方形的边界运动一周,再回到
出发,沿正方形的边界运动一周,再回到 ![]() 点.若点
点.若点 ![]() 的路程为
的路程为 ![]() ,点
,点 ![]() 到顶点的距离为
到顶点的距离为 ![]() ,求
,求 ![]() 两点间的距离
两点间的距离 ![]() 与点
与点 ![]() 的路程
的路程 ![]() 之间的函数关系式.
之间的函数关系式.
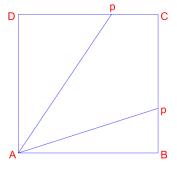 分析:由于点
分析:由于点
![]() 分别在
分别在 ![]() 上移动时,相应距离计算方法是不同的,故需分类讨论.
上移动时,相应距离计算方法是不同的,故需分类讨论.
解:(1)当点 ![]() 在
在 ![]() 边上即
边上即 ![]() 时,
时, ![]() 也就是
也就是 ![]() ;
;
(2)当点 ![]() 在
在 ![]() 边上时,即
边上时,即 ![]() 时,
时, ![]() ,由勾股定理得
,由勾股定理得
![]() .
.
(3)当点 ![]() 在
在 ![]() 边上即
边上即 ![]() 时,
时, ![]() ,
由勾股定理得
,
由勾股定理得
![]() .
.
(4)当点 ![]() 在
在 ![]() 边上即
边上即 ![]() 时,有
时,有 ![]() .
.
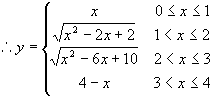 .
.
说明:几何应用问题要注意实际问题对定义域的限制条件.对分界点的讨论应做到不重不漏.
例2.将进货单价为20元的商品按30元一件销售时,一个月可卖400件.若这种商品的销售单价每变化1元,月销售量改变20件(降价时销售量增加,提价时销售量减少)为了获得最大利润,此商品的销售单价应定为多少元?
分析:首先可以根据题意自己选择自变量 ![]() (可以取提高的钱数也可选取销售单价)然后再把利润的计算搞清.利润=(原销售单价+提价-进货价)
(可以取提高的钱数也可选取销售单价)然后再把利润的计算搞清.利润=(原销售单价+提价-进货价) ![]() (原销售量-滞销量).
(原销售量-滞销量).
解:设销售单价提高 ![]() 元,则月滞销量为20
元,则月滞销量为20 ![]() 件.由题意得
件.由题意得 ![]()
即
![]() ,当
,当 ![]() 时,
时, ![]() ,此时
,此时 ![]()
![]() 当每件商品售价提高5元即销售价定为35元时,月利润最大,最大利润为4500元.
当每件商品售价提高5元即销售价定为35元时,月利润最大,最大利润为4500元.
说明:此题是商品销售的最典型问题.弄清各术语的意义及它们之间的关系是解决问题的关键.在正常情况下,上式中定义域的负值含义为降低,为零时,为不升不降.
例3.某渔场养鱼,第一年:鱼的重量增长200%,以后每年的重量增长率是前一年增长率的一半.
(1) 当饲养4年后,鱼的重量是原来的多少倍?
(2) 如果由于某种原因,每年损失预计重量的10%,那么经过多少年后鱼的总重量开始减少?
分析:在实际问题中有关增长率的问题是较常见的.要解决这类增长率问题通常都会用到与指数函数相关的函数式 ![]() ,其中
,其中 ![]() 是原来的基数,
是原来的基数, ![]() 为增长率,
为增长率, ![]() 为时间.
为时间.
解:(1)设鱼原来的重量为
![]() ,
, ![]() 年后鱼的重量为
年后鱼的重量为 ![]() ,则:
,则:
![]()
![]() .
.
故四年后的重量是原来重量的 ![]() 倍.
倍.
(2)由 ![]() ,得
,得 ![]() ,
, ![]() .
.
故经过五年后鱼的重量开始减少.
说明:对于增长率问题,可以先从一年一年的增长计算开始,在具体计算中再找出相应的规律列式计算.
例4.汽车在行驶中,由于惯性作用,刹车后还要继续向前滑行一段距离才能停住,我们把这段距离称为“刹车距离”.刹车距离是分析事故的一个重要因素,在一个限速40千米/小时以内的弯道上,甲乙两辆汽车相向而行,发现情况不对同时刹车,但还是相碰了.事发后现场测得甲车得刹车距离超过12米,乙车刹车距离略超过10米,又知甲乙两种车型的刹车距离
![]() (米)与车速
(米)与车速 ![]() (千米/小时)之间分别有如下关系:
(千米/小时)之间分别有如下关系:
![]() ,
, ![]() ,问超速行驶应负主要责任的是谁?
,问超速行驶应负主要责任的是谁?
分析:此题关键在于题意的理解及向数学问题的转化.负主要责任即车速的比较应尽量列出关于车速的不等式即可.
解:据题意得 ![]()
(1)
和 ![]()
(2)
由(1)得 ![]() 或
或 ![]() ,由(2)得
,由(2)得 ![]() 或
或 ![]() .分别舍去负值可知
.分别舍去负值可知 ![]() 千米/小时
千米/小时 ![]() 千米/小时.两车相比,乙车超过限速应负主要责任.
千米/小时.两车相比,乙车超过限速应负主要责任.
例5.用汽船拖载重量都是 ![]() 且满载货物得小船若干只,在两港之间来回运送货物.若每次拖4只小船,则一天可来回16次,若每次拖7只小船,则一天可来回10次,且每天来回次数是每次所拖小船只数的一次函数,若每天每次所拖小船数不变,每天来回多少次,每次拖几只小船,才能使运货总重量达到最大,每天最大运货总重量是多少?
且满载货物得小船若干只,在两港之间来回运送货物.若每次拖4只小船,则一天可来回16次,若每次拖7只小船,则一天可来回10次,且每天来回次数是每次所拖小船只数的一次函数,若每天每次所拖小船数不变,每天来回多少次,每次拖几只小船,才能使运货总重量达到最大,每天最大运货总重量是多少?
分析:运货总重量与每天小船来回次数,每次所拖小船只数以及小船载重量有关.由于小船载重量为定值,所以具体求出每天来回次数与每次所拖小船只数的关系式是解决问题的关键.
解: 设汽船每次拖 ![]() 只小船,每天来回
只小船,每天来回 ![]() 次,每天的运货量为
次,每天的运货量为 ![]() .
.
由题意设 ![]()
![]() ,则有
,则有 ![]() 解得
解得 ![]()
![]() .于是
.于是 ![]() .
.
当 ![]() 时,
时, ![]() 此时
此时 ![]() .
.
因此每天来回12次,每次拖6只小船,使运货重量最大,最大为72
![]() .
.
说明:此题中所研究的函数与多个自变量有关,可以通过寻求这些变量间的关系代入后达到减少变量个数的目的,最终形成与元函数求最大(小)值的问题.
例6.工厂的质量检验车间积压着部分产品待检,与此同时,流水线传送带按定速度来待检产品.如果打开一部质检机,需半小时可使待检产品全部通过质量检验,同时打开两部质检机,只需10分钟便可将待检产品全部通过质量检验.现因生产需要在5分钟内将待检产品全部通过质量检验,此时最少要同时打开几部质检机?
分析:每部质检机每分钟质检产品件数,传送带每分钟送来的产品数是列式计算的关键.
解: 依题意,设积压的待检产品为 ![]() 件,每部质检机每分钟质检
件,每部质检机每分钟质检 ![]() 件,传来的待检产品每分钟增加
件,传来的待检产品每分钟增加 ![]() 件,则
件,则 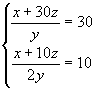 解得
解得 ![]() .
.
若同时打开3部质检机,质检时间
![]() ,将
,将 ![]() 代入得
代入得 ![]() ,若同时打开4部质检机,质检时间
,若同时打开4部质检机,质检时间 ![]() ,将
,将 ![]() 代入得
代入得 ![]() .
.
故最少要同时打开4部质检机才能在5分钟内将待检产品全部通过检验.
说明:对所列方程组,应将 ![]() 看作未知数求解,这也是处理多个变量问题的一种处理策略.
看作未知数求解,这也是处理多个变量问题的一种处理策略.