设为首页
设为首页
 加入收藏
加入收藏
例1. 求下列函数的定义域
(1)
![]() (2)
(2) ![]()
(3)
![]()
解:(1)由 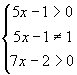 得
得 ![]() 且
且 ![]() .所求定义域为
.所求定义域为![]() .
.
(2)由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所求定义域为
,所求定义域为 ![]() .
.
(3)由 ![]() 得
得 ![]() ,当
,当 ![]() 时,
时, ![]() ,当
,当 ![]() 时,
时, ![]() .
.
所求定义域为当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() .
.
说明:注意对数函数的单调性也是与底数 ![]() 相关,但还必须同时注意保证真数有意义.
相关,但还必须同时注意保证真数有意义.
例2.
求函数 ![]() 的反函数.
的反函数.
分析:应首先按照求反函数的步骤去操作,求值域时应注意按复合函数求值域去操作.
解: 由 ![]()
![]() 得,
得, ![]() .
.
![]() ,又
,又 ![]()
于是有 ![]() .又
.又 ![]() 的值域为
的值域为 ![]() ,
,
![]() 所求反函数为
所求反函数为 ![]() .
.
例3. 比较下列各组数的大小:
(1)
![]() 与
与 ![]() (2)
(2) ![]() ,
, ![]() ,
, ![]()
(3)若 ![]() .
.
分析:比较两个对数形的数若同底可利用对数函数的单调性,若不同底可以借助常数为媒介搭桥比较也可以借助对数函数图象来确定对数值的取值范围进行比较.
解:(1)由 ![]() 在
在 ![]() 上单调递增,且
上单调递增,且 ![]() ,故
,故 ![]() <
< ![]() .
.
(2)
![]() ,而
,而 ![]() ,
, ![]() ,
,
![]()
(3)令 ![]() ,由
,由 ![]() 可知
可知 ![]() 即
即 ![]() .
.
则 ![]() ,
, ![]() ,
,
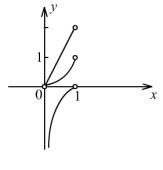
在同一坐标系下画出这三个函数的图象, 如图示:
可知 ![]() 最大,
最大, ![]() 最小,即
最小,即 ![]() .
.
例4.
已知函数 ![]() ,(
,( ![]() 且
且 ![]() .试写出函数的单调区间.
.试写出函数的单调区间.
分析:欲求出函数的单调区间,必须由条件先确定底数 ![]() 的情况,再结合函数是偶函数求出单调区间.
的情况,再结合函数是偶函数求出单调区间.
解:由 ![]() 得
得 ![]() 的定义域为
的定义域为 ![]() ,
,
且 ![]() ,
,
故 ![]() 为偶函数.
为偶函数. ![]() .又
.又![]()
由 ![]() 可知
可知 ![]() .
.
![]() =
= 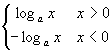 ,在
,在 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数.
上是减函数.
说明:此题对底数范围的确定是函数单调性的反用,而且在自变量的比较时,应让它们处在函数的同一单调区间内.
例5.
已知 ![]() ,求
,求 ![]() 的最大值和相应的
的最大值和相应的 ![]() 值.
值.
分析:求 ![]() 的最大值需先解决两个问题,一是找出其表达式,二是求出它的定义域.
的最大值需先解决两个问题,一是找出其表达式,二是求出它的定义域.
解: ![]() ,
, ![]() =
= ![]() .
.
![]()
![]() 的定义域为
的定义域为 ![]()
![]() 解得
解得 ![]() ,
, ![]() .
.
故 ![]()
![]() ,当
,当 ![]() 时,
时, ![]() 此时
此时 ![]() .
.
说明:此题求解的关键是 ![]() 的定义域的确定,它应使
的定义域的确定,它应使 ![]() 中的
中的 ![]() 和
和 ![]() 都有意义,所以应有
都有意义,所以应有 ![]() 和
和 ![]()
![]() 同时成立.
同时成立.
例6.
设函数 ![]() ,若
,若 ![]() 的值域为
的值域为 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
分析:由值域为 ![]() 和对数函数的单调性可将问题转化为
和对数函数的单调性可将问题转化为 ![]() 能取遍所有正实数的问题.
能取遍所有正实数的问题.
解:令 ![]() ,依题意
,依题意 ![]() 应取遍一切正实数即函数值域是正实数集的子集.则有
应取遍一切正实数即函数值域是正实数集的子集.则有 ![]() 或
或 ![]() ,解得
,解得 ![]() .
.
说明:将非常规问题通过等价变换转化为常规问题是处理陌生问题的重要手段.
例7.
设函数 ![]() 在
在 ![]() 上函数值恒有
上函数值恒有 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
分析:此题中 ![]() 对
对 ![]()
![]() 恒成立的问题,是无数多个不等式的成立问题应借助函数思想,利用函数的最值,将其转化为有限个不等式的求解问题.
恒成立的问题,是无数多个不等式的成立问题应借助函数思想,利用函数的最值,将其转化为有限个不等式的求解问题.
解:问题等价于对任意 ![]()
![]()
![]() 或
或 ![]() .
.
![]() 的最小值
的最小值 ![]() 或
或 ![]() 的最大值
的最大值 ![]() .
.
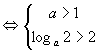 或
或 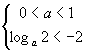 .
.
![]() 或
或 ![]() .
.
![]() 所求
所求 ![]() 的取值范围是
的取值范围是