第七节 对数

例1．求下列各式中的 ．

　　(1) ;              (2) ;  

　　(3) ;  　　(4) ;  

 　　(5) ．

　　分析：根据式中 的位置或转化成指数式计算或利用对数性质进行计算．

　　解： (1) ．

　　(2) ，得 ．

　　(3) ，得 或 ．

　　(4)由对数性质得 ．

　　(5)由对数性质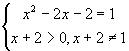得 解得 ．

　　证明：对数式的运算除了注意使各量都有意义为前提，还要注意指对之间的互化互助．

例2．已知 ，求 的值．

　　分析：根据复合函数的概念，结合换元法可以直接求值，当然也可以先求出 的解析式再求 的值．

　　解：法一令 则 ， ． ．

　　法二由 ，得 ， ．

　　说明：此题以函数概念为背景，实际考察对数的运算法则的使用．

例3．计算

　　(1) ;   (2)  ;    (3) ．

　　分析：对数运算法则是解决这类运算的重要工具，除此之外还需用到有关指数幂的运算法则进行计算．

　　解：(1)原式= ．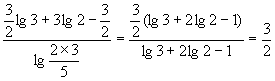

　　(2)原式=

　　　　　　=

　　　　　　= ．

　　(3)原式= ．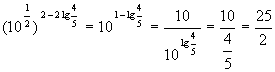

　　说明：第(2)小题的运算除利用法则外，有一定的设计性，主导思想是减少对数值的个数．此提在减少量的思想指导下，只剩一种元“ ”是最理想的状态．

例4．(1)已知 ，则 =__________．

　　(2)设 ，则 的值为_____．

　　(3)已知 则 的值为___________．

　　分析：此组小题主要将指对运算混合在一起，注意各自法则的正确使用．

　　解： (1)由性质得 又由性质得 ，由定义得 ． ．

　　(2)由已知得 ．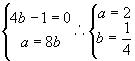

　　 = ．

　　(3)将其改写为指数式为 ， = ．

　　说明： 利用指数对数的对立统一性，注意运算形式的选择，以简化计算．

例5．已知 ， ，试用 的式子表示 ．

　　分析：求以 表示 的式子，实际上是寻找 和 之间的关系所以应将三个真数尽量化整并化小，便于寻找关系．

　　解：       (1)

　　                         (2)

　　由(1)(2)解得 ， ．

　　 = ．

　　说明：本题的求解中，分解化简和方程思想的运用在处理很多问题中具有一般性．

　　例6．对于正整数 和实数 ， ， = ，求 的值．

　　分析：可先从条件中化去 ，的到含有 的方程，转化条件可以利用指对互化来完成．

　　解：在 中，两边取对数得 ， ．

　　同理由 和 得 ，又 =

　　 即 ．又 ，可分为三种情况：

　　如果 由 得 (舍去)

　　如果 ，得 ．

　　如果 ，此时 无整数解．

　　说明：对所给条件两边同时取对数是化简条件向指数转化的重要手段，且这里对 情况的讨论也要有主有次，抓住一个为主元，进行讨论即可．

例7．已知函数 满足 ．且对一切实数 都有 ，求实数 的值．

　　分析：这是一道函数与不等式结合的题目需确定 的类型，再根据条件求解．

　　解：由 得       (1)，

　　由 得    (2)

　　(2)对任意 恒成立的条件是△= ．将(1)中 代入得 解得 ．

　　说明：此题中“对一切实数 都有 恒成立”的问题的转化，必须保证其等价性．

返回页首