 设为首页
设为首页
 加入收藏
加入收藏
典型例题(例4~例7)
例4 (1)函数
![]() 的图象一定过____________象限.
的图象一定过____________象限.
(2)函数 ![]() 的图象一定过定点
的图象一定过定点 ![]() ,则
,则 ![]() 点的坐标是_________.
点的坐标是_________.
(3)函数 ![]() 与___________的图象关于
与___________的图象关于 ![]() 轴对称.
轴对称.
分析:此题涉及有关图象变换,搞清图象平移和对称变换是解决此题的关键.
解:
(1) ![]() =
= ![]() ,它可以看作是指数函数
,它可以看作是指数函数 ![]() 图象作关于
图象作关于 ![]() 轴对称的图象,因此一定过第三象限和第四象限.
轴对称的图象,因此一定过第三象限和第四象限.
(2)
![]() 的图象可以看作把
的图象可以看作把 ![]() 的图象向右平移一个单位再向上平移3个单位而得到,且
的图象向右平移一个单位再向上平移3个单位而得到,且
![]() 一定过点
一定过点 ![]() ,则
,则 ![]() 应过点
应过点 ![]() .
.
(3)图象与
![]() 关于
关于 ![]() 轴对称的函数为
轴对称的函数为 ![]() .
.
说明:通过此题要求学生明确
![]() 与
与 ![]() 两个函数图象之间的关系及体现在图象上任意一点的坐标之间的变化规律.
两个函数图象之间的关系及体现在图象上任意一点的坐标之间的变化规律.
例5.
(1)函数 ![]() 的单调递增区间是_______________.
的单调递增区间是_______________.
(2)函数
![]() 的值域为___________.
的值域为___________.
分析:应利用换元法研究这类题目,而且要注意二次函数相关知识的配合使用.
解:
(1)令 ![]() ,显然当
,显然当 ![]() 时,由
时,由 ![]() 是增函数,此函数是单调递增的.
是增函数,此函数是单调递增的.
(2)令
![]() ,由
,由 ![]() ,得
,得 ![]() .
.
则
![]()
![]() .
.
当
![]() 即
即 ![]() 时,
时, ![]() 有最小值
有最小值 ![]() ,当
,当 ![]() 即
即 ![]() 时,
时, ![]() 有最大值57.
有最大值57.
![]() 函数的值域为
函数的值域为 ![]() .
.
说明:第(2)小题通过换元把问题转化为闭区间上二次函数的值域问题,这种转化的方法是处理类似问题非常重要的方法,应引起关注,且换元时应注意中间变量的取值范围.
例6. 世界人口已超过56亿,若按千分之一的年增长率计算,则两年增长的人口相当于一个( ).
分析:这是指数函数的应用问题,根据题意列出函数解析式后再进行相应的计算.
解:
两年增长的人口应为560000(1+1‰) ![]() ≈1120(万),所以应选
≈1120(万),所以应选 ![]() .
.
说明:与指数函数相关的应用问题较多,如放射性物质的蜕变,人口增长,利率等,遇到类似问题时,应能主动调动指数函数相关知识来解决.
例7.已知
![]() ,试把
,试把 ![]() 用含
用含 ![]() 的式子表示出来,并化简.
的式子表示出来,并化简.
分析:此题涉及指数式的变换和分类讨论的使用.
解:
由 ![]() 可知
可知 ![]() ,
, ![]()
![]()
=
![]() ,
, ![]()
![]()
当![]() 时,若
时,若 ![]() ,则
,则 ![]() ,此时
,此时 ![]() ,
,
若 ![]() ,则
,则 ![]() ,此时
,此时 ![]() .
.
当![]() 时,
时, ![]() .
.
当 ![]() 时, 若
时, 若 ![]() ,则
,则 ![]() ,此时
,此时 ![]() ,
,
若
![]() ,则
,则 ![]() ,此时
,此时 ![]() .
.
说明:此题中涉及对根式的化简,绝对值的概念及指数函数单调性的使用,特别是对
![]() 和
和 ![]() 的讨论要分清楚.
的讨论要分清楚.
典型例题(例1~例3)
例1. 求下列函数的定义域
(1)
![]() ; (2)
; (2) ![]()
(3)
![]() ; (4)
; (4) ![]() .
.
分析:求定义域时要特别注意与指数式有关的式子有意义的条件.
解:
(1) ![]() ; (2)由
; (2)由
![]() 得
得 ![]() ; (3)
; (3) ![]() ;
;
(4)由
![]() 得
得 ![]() ,当
,当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]() .
.
说明:在这种题目中若遇到底数含有字母的不等式的求解时,注意分为
![]() 和
和 ![]() 两种情况进行讨论,求解时,可借助相应的指数函数图象来帮忙.
两种情况进行讨论,求解时,可借助相应的指数函数图象来帮忙.
例2. 比较下列各组数的大小:
(1)
![]() 和
和 ![]() ; (2)
; (2)
![]() 和
和 ![]() ;
;
(3)
![]() 和
和 ![]() ;
(4)
;
(4) ![]() 和
和 ![]() ,
, ![]() .
.
分析:当两个幂形数底数相同时,要比较这两个数的大小可根据它们的特征构造相应的指数函数,借助函数的单调性来比较大小.
解:
(1) ![]() 在
在 ![]() 上是减函数,又
上是减函数,又 ![]() ,故
,故 ![]() <
< ![]() .
.
(2)
![]() =
= ![]() ,由
,由 ![]() 的单调性可得,
的单调性可得, ![]() >
> ![]() 即
即 ![]() >
> ![]() .
.
(3)由
![]() >1而
>1而 ![]() <1,可知
<1,可知 ![]() >
> ![]() .
.
(4)当
![]() 时,
时, ![]() <
< ![]() ,当
,当 ![]() 时,
时, ![]() >
> ![]() .
.
说明:此题中第(3)小题的两个数不能看成某个指数函数的两个函数值,此时可以借助一些特殊数如0或1来搭桥间接比较两个数的大小,而(2)小题则可以通过指数运算化为底数相同的两个幂,可构造指数函数来比较大小.
例3.(1)指数函数①
![]() ②
② ![]() 满足不等式
满足不等式 ![]() ,则它们的图象是 (
).
,则它们的图象是 (
).
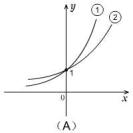
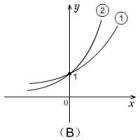
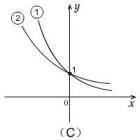
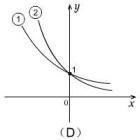
分析:此题应首先根据底数的范围判断图象的升降性,再根据两个底数的大小比较判断对应的曲线.
解:由
![]() 可知①②应为两条递减的曲线,故只可能是
可知①②应为两条递减的曲线,故只可能是 ![]() 或
或 ![]() ,进而再判断①②与
,进而再判断①②与 ![]() 和
和 ![]() 的对应关系,此时判断的方法很多,不妨选特殊点法,令
的对应关系,此时判断的方法很多,不妨选特殊点法,令
![]() ,①②对应的函数值分别为
,①②对应的函数值分别为
![]() 和
和 ![]() ,由
,由 ![]() 可知应选
可知应选 ![]() .
.
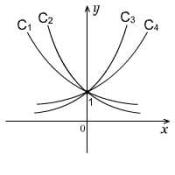 (2)曲线
(2)曲线 ![]() 分别是指数函数
分别是指数函数 ![]() ,
, ![]() 和
和 ![]() 的图象,则
的图象,则 ![]() 与1的大小关系是
( ).
与1的大小关系是
( ).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
分析:首先可以根据指数函数单调性,确定
![]() ,在
,在 ![]() 轴右侧令
轴右侧令 ![]() ,对应的函数值由小到大依次为
,对应的函数值由小到大依次为 ![]() ,故应选
,故应选 ![]() .
.
说明:这种类型题目是比较典型的数形结合的题目,第(1)题是由数到形的转化,第(2)题则是由图到数的翻译,它的主要目的是提高学生识图,用图的意识.