 设为首页
设为首页
 加入收藏
加入收藏
典型例题(例1~例3)
例1.下列说法中正确的是( ).
(A)-2是16的四次方根
(B)正数的 ![]() 次方根有两个
次方根有两个
(C)
![]() 的
的 ![]() 次方根就是
次方根就是 ![]() (D)
(D) ![]()
分析:从
![]() 次方根和
次方根和 ![]() 次根式的概念入手,认清各概念与各符号之间的关系.
次根式的概念入手,认清各概念与各符号之间的关系.
解:
(1)是正确的.由 ![]() 可验证.
可验证.
(2)不正确,要对
![]() 分奇偶讨论.
分奇偶讨论.
(3)不正确,
![]() 的
的 ![]() 次方根可能有一个值,可能有两个值,而
次方根可能有一个值,可能有两个值,而 ![]() 只表示一个确定的值它叫根式.
只表示一个确定的值它叫根式.
(4)正确,根据根式运算的依据,当
![]() 为奇数时,
为奇数时, ![]() 是正确的,当
是正确的,当 ![]() 为偶数时,若
为偶数时,若 ![]() ,则有
,则有 ![]() ,综上,当
,综上,当 ![]() 时,无论
时,无论 ![]() 为何值均有
为何值均有 ![]() 成立.
成立.
说明:此题主要目的是分清 ![]() 次方根是什么和有几个,进一步明确根式进行简单运算的依据.
次方根是什么和有几个,进一步明确根式进行简单运算的依据.
例2.求下列各式的值.
(1)
![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() ; (4)
; (4)
![]() .
.
分析:依照根式运算的两条规律,进行运算即可.
解:(1)
![]()
![]() .
.
(2)
![]() =
= ![]() .
.
(3)
![]() =
= ![]() .
.
(4)
![]()
![]() .
.
说明:根式运算要注意分清 ![]() 与
与 ![]() ,此外对于
,此外对于 ![]() 的运算可以记为
的运算可以记为 ![]() =
=  ,这样先根据
,这样先根据 ![]() 的奇偶处理根式,再根据
的奇偶处理根式,再根据 ![]() 的正负处理绝对值比较方便.
的正负处理绝对值比较方便.
例3.求下列各式的值.
(1)
![]()
![]()
![]() ;
;
(2)
![]() ;
;
(3)
![]() .
.
分析:依照分数指数幂的运算法则,并结合概念来完成运算.
解:(1)原式=
![]() .
.
(2)原式=
![]()
= ![]() .
.
(3)原式=
![]()
=
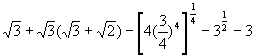
=
![]() =
= ![]() .
.
说明:在分数指数幂的运算中要注意把法则和概念结合起来,进行运算,并能根据具体题目选择最恰当的形式来完成运算.
典型例题(例4~例6)
例4.计算下列各式
(1)
![]() ;
;
(2)
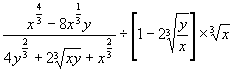 .
.
分析:这种类型的题目属于混合运算,运算的关键是顺序,先乘方,再乘除,最后做加减.
解:(1)原式=
![]()
=
![]() =
= ![]()
![]() .
.
(2)原式=
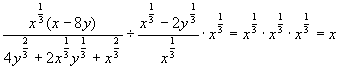 .
.
说明:这类题目在运算上除了要注意运算顺序以外,还应注意将系数和字母分开计算.
例5.已知
![]() ,求
,求 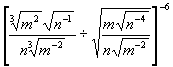 的值.
的值.
分析:一般根式的运算都化成分数指数幂的运算会比较方便.
解:原式=
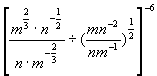 =
= ![]()
当
![]() 时,原式=
时,原式= ![]() .
.
说明:这种类型的求值问题,一般不是直接将 ![]() 值代入,而是先化简所求式,再代入求值.
值代入,而是先化简所求式,再代入求值.
例6.设
![]() ,求
,求 ![]() 的值.
的值.
分析:这里首先应把 ![]() 看作一个整体去寻求与已知条件的联系,再把已知利用乘法公式表示成关于
看作一个整体去寻求与已知条件的联系,再把已知利用乘法公式表示成关于
![]() 的方程,解此方程即可.
的方程,解此方程即可.
解:由乘法公式
![]() ,又
,又 ![]() .
.
故
![]() ,令
,令 ![]() =
= ![]() ,则方程变形为
,则方程变形为 ![]()
解方程得
![]() 或
或 ![]() .若
.若 ![]() ,则有
,则有 ![]() =-1,此时方程无解,故
=-1,此时方程无解,故 ![]() 舍去.
舍去.
![]()
![]() ,即
,即 ![]() =2.
=2.
说明:此种类型的求值题往往需要将指数式的变形与方程思想的应用结合起来.