 设为首页
设为首页
 加入收藏
加入收藏
典型例题(例1~例4)
例1 给出下列函数的图象,指出函数的单调区间,并指明其单调性.
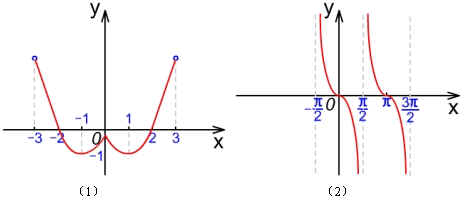
分析:通过图象直观观察其升降来判断其增减性,但必须注意区间端点的取舍要合理.
解:图(1)中 ![]() 的单调区间有
的单调区间有 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .其中在
.其中在 ![]() 和
和 ![]() 上是减函数,在
上是减函数,在 ![]() 和
和 ![]() 上是增函数.
上是增函数.
图(2)中 ![]() 的单调区间有
的单调区间有 ![]() 和
和 ![]() ,其中在
,其中在 ![]() 和
和 ![]() 上都是减函数.
上都是减函数.
说明:图(1)中 ![]() 和
和 ![]() 不在定义域内,因此写单调区间时在这两个点上必须写成“开”而其余端点写成“开”或“闭”均可.图(2)中虽在两个区间上均为减区间,但不能把两个区间并起来.
不在定义域内,因此写单调区间时在这两个点上必须写成“开”而其余端点写成“开”或“闭”均可.图(2)中虽在两个区间上均为减区间,但不能把两个区间并起来.
例2 用函数单调性定义证明:
(1)
![]() 为常数)在
为常数)在 ![]() 上是增函数.
上是增函数.
(2)
![]() 在
在 ![]() 上是减函数.
上是减函数.
分析:虽然两个函数均为含有字母系数的函数,但字母对于函数的单调性并没有影响,故无须讨论.
证明: (1)设 ![]() 是
是
![]() 上的任意两个实数,且
上的任意两个实数,且 ![]() ,
,
则 ![]()
![]()
![]()
=
![]()
由 ![]() 得
得
![]() ,由
,由
![]()
![]() 得
得 ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]()
![]() 即
即 ![]() .
.
于是 ![]() 即
即
![]() .
.
![]()
![]() 在
在 ![]() 上是增函数.
上是增函数.
(2)
设 ![]() 是
是
![]() 上的任意两个实数,且
上的任意两个实数,且 ![]() ,
,
则 ![]()
![]()
由
![]() 得
得
![]() ,由
,由
![]()
![]() 得
得 ![]()
![]() .又
.又 ![]() ,
, ![]() .
.
于是 ![]() 即
即
![]() .
.
![]()
![]() 在
在 ![]() 上是减函数.
上是减函数.
说明:由(1)中所得结论可知二次函数的单调区间只与对称轴的位置和开口方向有关,与常数 ![]() 无关.若函数解析式是分式,通常变形时需要通分,将分子,分母都化成乘积的形式便于判断符号.
无关.若函数解析式是分式,通常变形时需要通分,将分子,分母都化成乘积的形式便于判断符号.
例3 函数 ![]() 在
在 ![]() 上是减函数,求
上是减函数,求 ![]() 的取值集合.
的取值集合.
分析:首先需要对 ![]() 前面的系数进行分类讨论,确定函数的类型,再做进一步研究.
前面的系数进行分类讨论,确定函数的类型,再做进一步研究.
解:当 ![]() 时,函数此时为
时,函数此时为 ![]() ,是常数函数,在
,是常数函数,在 ![]() 上不具备增减性.
上不具备增减性.
当 ![]() 时,
时, ![]() 为一次函数,若在
为一次函数,若在 ![]() 上是减函数,则有
上是减函数,则有 ![]() ,解得
,解得![]() .故所求
.故所求 ![]() 的取值集合为
的取值集合为 ![]() .
.
说明:此题虽比较简单,但渗透了对分类讨论的认识与使用.
例4 下列函数是否具有奇偶性.
(1)
![]() ;
(2)
;
(2) ![]() ;
;
(3)
![]() ;
(4)
;
(4) ![]() .
.
分析:根据定义,检验 ![]() 与
与 ![]() 的关系,同时注意定义域.
的关系,同时注意定义域.
解: (1) ![]()
![]() .
. ![]()
![]() 是奇函数.
是奇函数.
(2)
![]() .
. ![]()
![]() 是偶函数.
是偶函数.
(3)由于定义域 ![]() 不关于原点对称,故
不关于原点对称,故 ![]() 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(1)
![]() 的定义域为
的定义域为 ![]() 且
且 ![]() ,是关于原点对称的,且有
,是关于原点对称的,且有 ![]() 和
和
![]() 同时成立, 故
同时成立, 故 ![]() 既是奇函数又是偶函数.
既是奇函数又是偶函数.
典型例题(例5~例7)
例5 已知函数 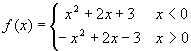 .判断
.判断 ![]() 的奇偶性,并加以证明.
的奇偶性,并加以证明.
分析:这是一个分段函数,且每一段的解析式都比较熟悉,所以在判断其奇偶性时可以借助函数图象观察图象的对称性而得出结论,但要证明则只能依靠定义.
解: ![]() 为奇函数.下面给出证明.当
为奇函数.下面给出证明.当 ![]() 时,
时,
![]() ;
;
当 ![]() 时,
时,![]()
综上 ![]() 为奇函数.
为奇函数.
说明:根据定义进行证明时,必须分别证明 ![]() 和
和 ![]() 时均有
时均有 ![]() 成立,二者缺一不可.
成立,二者缺一不可.
例6 若函数 ![]() 在
在 ![]() 上是奇函数,试确定
上是奇函数,试确定 ![]() 的解析式.
的解析式.
分析:欲求 ![]() 的值,根据方程思想只需找出关于
的值,根据方程思想只需找出关于 ![]() 的两个独立条件列方程,而列方程的依据是
的两个独立条件列方程,而列方程的依据是 ![]() 是
是 ![]() 上的奇函数.
上的奇函数.
解:在 ![]()
![]() 中,由
中,由 ![]() 得
得 ![]() ,由
,由
![]() 得
得 ![]() ,得
,得 ![]() ,
,
![]() .
.
说明:由奇函数的定义得到
![]() 的制约条件时,应利用一般与特殊的思想让
的制约条件时,应利用一般与特殊的思想让 ![]() 取某两个特殊值即可.这个想法是建立在对奇函数定义中恒等关系的理解.
取某两个特殊值即可.这个想法是建立在对奇函数定义中恒等关系的理解.
例7 已知函数 ![]() 与
与 ![]() 的定义域都是
的定义域都是 ![]() ,值域分别是
,值域分别是 ![]() 与
与 ![]() ,在
,在 ![]() 上
上 ![]() 是增函数而
是增函数而 ![]() 是减函数,
是减函数,
求证: ![]() 在
在 ![]() 上为减函数.
上为减函数.
分析:证明的依据应是减函数的定义.
证明:设 ![]() 是
是 ![]() 上的任意两个实数,且
上的任意两个实数,且 ![]() ,
,
则 ![]()
![]()
![]()
![]()
![]() 是
是 ![]() 上的增函数,
上的增函数, ![]() 是
是 ![]() 上的减函数,且
上的减函数,且 ![]() .
.
![]()
![]() ,
, ![]() 即
即
![]() ,
, ![]() .
.
又 ![]() 的值域为
的值域为
![]() ,
, ![]() 的值域为
的值域为 ![]() ,
,
![]() .
.
![]()
![]() 即
即 ![]()
![]()
![]() 在
在 ![]() 上为减函数.
上为减函数.
说明:此题涉及抽象函数的有关证明,要求较高,此外在 ![]() 的变形中涉及到增减项的技巧,它也应是源于单调性只能比较同一个函数的某两个函数值,必须构造出
的变形中涉及到增减项的技巧,它也应是源于单调性只能比较同一个函数的某两个函数值,必须构造出![]() 与
与 ![]() 的差和
的差和 ![]() 与
与 ![]() 的差.
的差.