第八节 充分条件与必要条件

典型例题

　　例1 指出下列各组命题中， 是 的什么条件（在“充分而不必要条件”“必要而不充分条件”“充要条件”“既不充分也不必要条件”中选出一种）。

　　（1） ：四边形对角线互相平分； ：四边形是矩形。

　　（2） ： ； ：抛物线 过原点。

　　（3） ： ； ： 。

　　（4） ：方程 有一根为1； ： 。

　　（5） ： ； ：方程 有实根。

　　

　　解：（1）四边形对角线互相平分 四边形是矩形。四边形是矩形 四边形对角线互相平分。所以 是 的必要而不充分条件。

　　（2） 抛物线 过原点，

　　抛物线 过原点 。

　　所以 是 的充要条件。

　　（3） 。

　　所以 是 的充分而不必要条件。

　　（4）方程 有一根为 。

 方程 有一根为1。

　　所以 是 的充要条件。

　　（5） 方程 有实根，方程 有实根 。

　　所以 是 的充分而不必要条件。

　　（6）利用集合的图示法（图1—13），知

　　

　　所以 是 的充要条件。

　　注意，第（5）小题也可从集合观点入手研究其充分必要性。实际上，

 ： ，

 ： 。

　　因为 ，所以 是 的充分而不必要条件。请用集合观点解答第（3）小题。

　　例2 已知关于 的一元二次方程（ ）

                      ①

             ②

　　求方程①和②的根都是整数的充要条件。

　　解  方程①有实数根的充要条件是 ，解得 ；

　　方程②有实数根的充要条件是 ，解得 。

　　所以 。而 ，得 ，或 ，或 。

　　当 时，方程①为 ，无整数根；

　　当 时，方程②为 ，无整数根；

　　当 时，方程①为 ，方程②为 ，①和②的根都是整数。

　　从而，①和②的根都是整数 ；反之， ①和②的根都是整数。

　　所以方程①和②的根都是整数的充要条件是 。

　　例3 设关于 的一元二次不等式， 对一切实数均成立，求 的取值范围．

　　解：一元二次不等式 ，对一切 恒成立 二次函数 的图像全在 轴上方 ．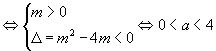

　　注：这里“ 的取值范围： ”就是“二次不等式 对一切实数 都成立”的充要条件．

　　有些问题（如求字母 的取值范围），我们必须通过等价变换，才能获得正确结果，这里的“等价变换”与“充要条件”是紧密相连的．我们所熟悉的解方程（或不等式）的过程，实质上是等价变换的过程．

　　例4 “ 且 为真”是“ 或 为真”的（      ）

　　（A）充分不必要条件．              （B）必要不充分条件．

　　（C）充要条件．                    （D）既不充分又不必要条件．

　　解：“ 且 为真”，就是 和 都为真，所以 或 为真，即 且 为真 或 为真．

　　“ 或 为真”，即 为真或 为真， 与 不一定同时为真，所以， 或 为真 且 为真．

　　所以“ 且 为真”是“ 或 为真”的充分不必要条件．

　　例5 若甲是乙的充分条件，乙是丙的充要条件，丙是丁的必要条件，丁是乙的必要条件，问甲是丙的什么条件？乙是丁的什么条件？

　　解：由题意，分析如下图所示。

　　根据图示得：甲是丙的充分条件，乙是丁的充要条件．

　　常见错误及分析：

　　错解1：由图知，甲是丙的充分不必要条件，产生错误的原因是把“甲 乙”理解成了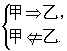

　　错解2：判为“乙是丁的充分条件”．产生错误的原因是只看出“ ”，而没有根据推理“ ”得出“ ”．

　　例6  已知 ： ； ： ．若 是 的必要而不充分条件，求实数 的取值范围．

　　点拨  可以有两个思路：

　　（1）先求出 和 ，然后根据 ， ，求得 的取值范围；

　　（2）若原命题为“若 ，则 ”，其逆否命题是“若 则 ”，由于它们是等价的，可以把求 是 的必要而不充分条件等价转换为求 是 的充分而不必要条件．

　　解法一  求出 ： 或 ，

　　　　　           ： 或 ．

　　由 是 的必要而不充分条件，知B A，它等价于

　　　　                  

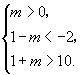
　　同样解得 的取值范围是 ．

　　解法二  根据思路二， 是 的必要而不充分条件，等价于 是 的充分而不必要条件．设

 ： ；

 ： ；

　　所以，A B，它等价于

　　                   

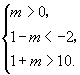
　　同样解得 的取值范围是 ．

返回页首