第十四节 两圆的公切线

典型例题

　　例1、如图，半径分别为3、1的⊙O₁与⊙O₂外切，一直线分别切它们于A、B，又交O₁O₂于．求：①切线AB长；②∠C的度数．

　　分析：首先想到切线性质，故连结O₁A、O₂B，得直角梯形AO₁O₂B．一般要把它分解成一个直角三角形和一个矩形，再用其性质．

　　解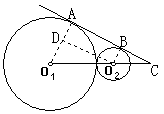：（1）连结O₁A、O₂B，作O₂D∥BA交O₁A于D．

　　则得Rt△O₂DO₁和矩形ADO₂B．

　　∵ AD=O₂B=1，　　O₁A=3

　　∴O₁D=3-1=2　　∵O₁O₂=3+1=4，

　　AB= O₂D= ．

　　（2）由（1）知O₁D=2，O₁O₂=4，∴∠C=∠DO₂O₁=30°

　　说明：（1）求外公切线长，应用切线性质、构造三角形；（2）添加辅助线的方法．

　　例2 如图，⊙O₁、⊙O₂的半径分别为4、5，O₁O₂=15，内公切线AB交O₁O₂于C．

　　求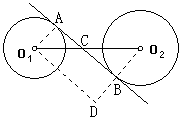：①AB长；②sin∠ACO₁的值．

　　解：（1）连结O₁A、O₂B，

　　作O₁D∥AB交O₂B延长线于D，

　　则得Rt△O₁DO₂，AO₁DB是矩形，

　　∵O₁D=4，O₂B=5，

　　∴O₂D=5+4=9

　　∴AB= O₁D= ．

　　（2）由（1）可知，sin∠ACO₁= sin∠O₂O₁D= ．

　　说明：（1）求内公切线长；（2）构造三角形、矩形，应用勾股定理、三角函数；（3）此题还可以通过△AO₁C∽△BO₂C，求出O₁A、O₂B，在求得．

　　例3、（福州市，2002）已知：半径不等的⊙O₁与⊙O₂相切于点P，直线AB、CD都经过切点P，并且AB分别交⊙O₁、⊙O₂于A、B两点，CD分别交⊙O₁、⊙O₂于C、D两点(点A、B、C、D、P互不重合)，连结AC和BD．

　　（1）请根据题意画出图形；

　　（2）根据你所画的图形，写出一个与题设有关的正确结论，并证明这个结论(结论中不能出现题设以外的其他字母)．

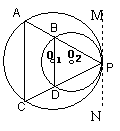
　　解：（1）如图所示．

　　（2）第一个结论：AC∥BD．

　　证明：过P作两圆的公切线MN，

　　∴∠MPA=∠C，∠NPB=∠D．

　　∵∠MPA=∠NPB，∴∠C=∠D，

　　∴AC∥BD．

　　第二个结论：△APC∽△BPD．

　　证明：过P作两圆的公切线MN，∴∠MPA=∠C，∠NPB=∠D．

　　∵∠MPA=∠NPB，∴∠C=∠D，又∠APC=∠BPD，∴△APC∽△BPD．

　　第三个结论：O₁、P、O₂三点共线（或连心线O₁O₂必过切点P）．

　　证明：∵①圆是轴对称图形，②相切的两个圆也组成轴对称图形，③连心线O₁O₂是两个圆的对称轴，∴O₁、P、O₂三点共线（或连心线O₁O₂必过切点P）

　　说明：①此题题型新颖，属于开放性题目，它源于教材P145练习第2题；②主要应用分类思想，作圆的公切线辅助线．

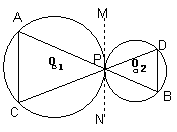
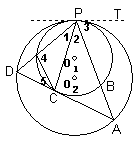
　　例4、已知：如图，⊙O₁与⊙O₂内切于点P，过点P的直线交⊙O₁于点D，交⊙O₂于点E；DA与⊙O₂相切，切点为C．

　　（1）求证：PC平分∠APD；

　　（2）若PE=3，PA=6，求PC的长．

　　证明：（1）过P作两圆的公切线PT，

　　∴∠TPC=∠4，∠3=∠D．

　　∵∠4=∠D+∠5，∴∠2+∠3=∠D+∠5，∴∠2=∠5

　　又DA与⊙O₂相切于点C，

　　∴∠5=∠1，∴∠1=∠2，即PC平分∠APD．

　　（2）∵DA与⊙O₂相切于点C，∴∠PCA=∠4．

　　由（1）知∠1=∠2，∴△PCA∽△PEC．

　　∴ ，即 ．∵PE=3，PA=6，∴ ，∴ ．

　　说明：①此题主要应用：切线的性质、弦切角、相似形以及作辅助线的方法；②此题得出∠1=∠2，在中考中是热点题目．

返回页首