第十二节 和圆有关的比例线段

典型例题

　　例1、某机械传动装置在静止状态时，如图所示．连杆PB与点B运动所形成的交于点A，测量得PA=4cm，AB=5cm，⊙O半径为4.5cm．求点P到圆心O的距离．

　　解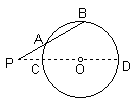：连结PO并延长，交⊙O于点C、D．

　　　根据切割线定理的推论，有PA·PB=PC·PD．

　　　∵PB=PA+AB=4+5=9，PC=PO-4.5，PD=PO+4.5，

　　　∴ ， ，

　　　∴OP= ．又OP为线段，取正数得OP=7.5（cm）

　　　∴点P到圆心O的距离为7.5（cm）．

　　说明：割线定理的在计算中的简单应用．

　　例3、已知：如图，AB是⊙O的弦，P是AB上的一点，AB＝10cm，PA＝4cm，OP＝5cm，求⊙O的半径．

　　分析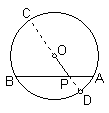：由P为AB上的一点，且巳知PA、PB故联想到相交弦定理，所以需把OP向两方延长，分别与圆相交，再利用相交弦定理解之．

　　解：向两方延长OP，分别交⊙O于C、D

　　　由相交弦定理有： BP·AP=CP·DP

　　　设CO=x，则

　　　

　　　解得： ，∵CO>0，∴CO=7（cm）

　　答：⊙O半径为7cm．

　　说明：①相交弦定理的简单应用；②作辅助线构成基本图形．

　　例3、已知：如图，在△ABC中，∠C=90°，BE是角平分线，DE⊥BE交AB于D，⊙O是△BDE的外接圆。

　　（1）求证AC是⊙O的切线；

　　（2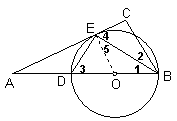）若AD=6，AE=6 ，求DE的长。

　　证明（1）：连结OE

　　　∵BE是∠ABC的平分线，∴∠1=∠2，

　　　又∵∠BED=∠C=90°，∴△BCE∽△BED，

　　　∴∠4=∠3，

　　　又∵OE=OB，∴∠1=∠5，∴∠4+∠5=∠1+∠3=90°，

　　　∴OE⊥AC，∴AC是⊙O的切线．

　　（2）∵AE是⊙O的切线，AE=6 ，AD=6，

　　　∴ ，∴ ．

　　　∴BD=AB-AD=12-6=6

　　　∵∠AED=∠ABE，∠A=∠A，∴△AED∽△ABE，∴

　　　设DE= ，BE=2x，∵ ，∴ ，

　　　得 （负的舍去），∴ ．

　　说明：①此题主要应用：切线的判定定理，切割线定理、相似形以及勾股定理以及相似形；

　　此题是与切割线定理有关的计算综合问题．

　　例4、如图，PA切⊙O于A，割线PBC交⊙O于B、C两点，D为PC的中点，连AD并延长交⊙O 于E，已知： ．

　　求证：（1）PA=PD；

　　（2） ．

　　分析：（1）易证∠PAD=∠PDA；

　　（2）关键在于利用线段之间的关系、等式性质，证出PB=BD．

　　证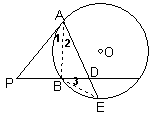明：(1)连结AB

　　　在△DBE和△BAE中 ，

　　　∵ ，即 ，

　　　又∠BED=∠AEB，∴△DBE∽△BAE

　　　∴∠2=∠3

　　　∵PA切⊙O于A，∴∠1=∠E

　　　又∠PAD=∠1+∠2，∠PDA=∠3+∠E．

　　　∴∠PAD=∠PDA，∴PA=PD．

　　(2)由切割线定理知， ，

　　　又PA=PD，PD=DC，　∴ ，

　　　∴PB=BD．

　　　又 (相交弦定理)，

　　　DC=2PB，BD=PB，∴ ．

　　说明：本题应用的知识点有：切割线定理、相交弦定理、弦切角定理、相似角形，利用等式性质证明线段的中点．

返回页首