第十一节 弦切角

典型例题

　　例1、如图，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB与⊙O相交于点E，AE平分∠CAB，且AE=2，求△ABC各边的长．

　　解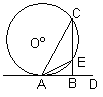：∵AD为⊙O的切线，∴∠BAE=∠C，

　　　∵AE平分∠CAB，∴∠BAC=2∠BAE，

　　　又∵∠C+∠BAC=90°，∴∠BAE=∠C=30°．

　　　则有BE=1，AB= ，BC=3，AC=2 ．

　　说明：此题应用弦切角、解直角三角形的知识，为基础题型．

　　例2、（吉林省，2000）如图，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，弦BD∥XY，AC、BD相交于点E．

　　（1）求证：△ABE≌△ACD；

　　（2）若AB=6cm，BC=4cm，求AE的长．

　　证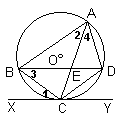明（1）：∵XY是⊙O的切线，∴∠1=∠2

　　　∵BD∥XY，∴∠1=∠3，∴∠2=∠3，

　　　∵∠3=∠4，∴∠2=∠4．

　　　∵∠ABD=∠ACD，又∵AB=AC．∴△ABE≌△ACD．

　　解（2）：∵∠3=∠2，∠BCE=∠ACB，∴△BCE∽△ACB

　　　∴ ，∴ ，即 ．∵AB=AC=6，BC=4，∴ ．∴ （cm）

　　说明：①此题利用平行线、弦切角、圆周角等角的转换；②建立方程求线段的长度．

　　例3、如图，P为⊙O的直径CB延长线上的一点，A为⊙O上一点，若 = ，AE交BC于D，且∠C= ∠PAD.

　　(1)求证：PA为⊙O的切线；

　　(2)若∠BEA=30°，BD＝1，求AP及PB长。

　　证明（1）：连结AO，∵ = ，BC为直径，

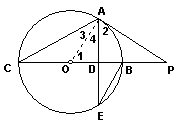　　　∴AE⊥BC，AD=DE， =  

　　　∵OA=OB，∴∠C=∠3，∴∠1=2∠C

　　　又∵∠C= ∠PAD，∴∠1=∠2

　　　∵∠1 +∠4=90°，∴∠2 +∠4=90°，∴PA⊥OA

　　　∴PA为⊙O的切线.

　　解（2）：在Rt△EBD中，∵∠BEA=30°，BD＝1. ∴BE=2，DE=

　　　在Rt△ODA和Rt△EBD中

　　　∠4=90°-∠1=90°-2∠C=90°-2∠E=30°=∠E，∠ODA=∠BDE，AD=ED

　　　∴Rt△ODA≌Rt△EBD，∴AD=DE= ，OD=BD=1，OA= BE=2.

　　　在Rt△OAP中，∵AD⊥OP，∴AD²=OD·DP，即 =1·DP，∴DP=3，∴BP=2 

　　　在Rt△ADP中

　　　根据勾股定理，得 AP= ．

　　说明：此题为综合型题目．它主要应用弦切角、垂径定理、切线的判定、三角形全等和方程思想．

返回页首