第一节 圆 1

典型例题

　　例1（天津2002中考试题）、已知AB、CD是⊙O的两条直径，则四边形ACBD一定是( )

　　（A）等腰梯形　（B）菱形　（C）矩形　（D）正方形

　　分析：问题的关键是圆的两条直径具备什么性质，构成特殊四边形的条件.

　　解：∵AB、CD是⊙O的两条直径，∴AB=CD，且AB、CD互相平分，

　　∴ACBD一定是矩形.应选（C）.

　　说明：①巩固圆的定义；②研究特殊四边形的顶点共圆问题.是圆与直线形知识的综合.（此题适宜第一课时用）

　　例2、已知等腰直角三角形ABC（如图），试取斜边AB上的一点为圆心画圆，使点A、B、C分别在所画的圆内、圆外和圆上．

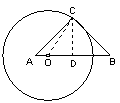
　　分析：确定一个圆有两个条件：圆心和半径，设选取圆心是点O，因为点C要在所画圆上，所以OC即为所画的圆的半径．（此题适宜第一课时用）

　　解：作中线CD，则AD=BD=CD，且CD⊥AB．

　　在AD上任取一点0，连接OC．以0为圆心，OC为半径画圆，这个⊙0即符合要求．这是因为AO＜AD=CD＜OC (垂线段最短)，所以点A在⊙0内．

　　BO=BD+DO=CD+DO＞CO(三角形两边之和大于第三边)，所以点B在⊙0外．

　　说明：该题可以激发学生的思维，提高学习兴趣；在画的过程中，复习和巩固知识，培养学生的思维能力.

　　例3、判断题

　　（1）直径是弦（ ）　　　　　　　　（2）弦是直径（ ）

　　（3）半圆是弧（ ）　　　　　　　　（4）弧是半圆（ ）

　　（5）长度相等的两段弧是等弧（ ）　（6）等弧的长度相等（ ）

　　解（略）

　　说明：通过原命题和逆命题的对比，深刻理解概念.另外这样的题目很多，这里知识抛砖引玉.（此题适宜第二课时用）

　　例4、已知：如图，两同心圆的直径AC、BD相交于O点.求证：AB=CD.

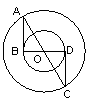
　　分析：证△AOB≌△COD即可.

　　证明：∵两同心圆的直径AC、BD相交于O点，

　　∴O点为两同心圆的圆心，∴OA=OC，OB=OD，

　　又∵∠AOB=∠COD

　　∴△AOB≌△COD（SAS）

　　∴AB=CD.

　　说明：此题目不难，但它是以“同心圆”为背景的，所以该题目重点不是证明过程，而是“同心圆”具备什么性质和特征.（此题适宜第二课时用）

返回页首