 设为首页
设为首页
 加入收藏
加入收藏
典型例题
【例】 设![]() 中,
中,![]() 于D,若
于D,若![]() ,解三角形ABC。
,解三角形ABC。
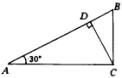
分析 “解三角形ABC”就是求出![]() 的全部未知元素。本题CD不是
的全部未知元素。本题CD不是![]() 的边,所以应先从Rt
的边,所以应先从Rt![]() 入手。
入手。
解:在Rt![]() 中,有
中,有
![]()
∴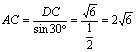
在Rt![]() 中,有
中,有
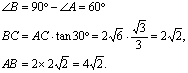
点拨 (1)应熟练使用三角函数基本关系式的变形,如
![]()
(2)平面几何中有关直角三角形的定理也可以结合使用,本例中“![]() ”就是利用“对30°角的直角边等于斜边的一半”这一定理。事实上,还可以用面积公式求出AB的值:
”就是利用“对30°角的直角边等于斜边的一半”这一定理。事实上,还可以用面积公式求出AB的值:
![]()
所以解直角三角形问题,应开阔思路,运用多种工具。
【例2】 在![]() 中,
中,![]() ,求
,求![]() 。
。
分析 (1)求三角形的面积一方面可以根据面积公式求出底和底上的高的长,也可以根据其中规则面积的和或差;
(2)![]() 不是直角三角形,可构造直角三角形求解。
不是直角三角形,可构造直角三角形求解。
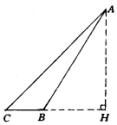
解:如图所示,作![]() 交CB的延长线于H,于是在
交CB的延长线于H,于是在![]() 中,有
中,有![]() ,且有
,且有
![]() ;
;
在![]() 中,
中,![]() ,且
,且
![]() ,
,
∴ ![]() ;
;
于是,有
![]() ,
,
则有
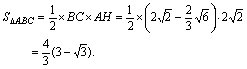
点拨 ![]() 还可以这样求:
还可以这样求:
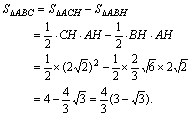
【例3】在![]() 中,
中,![]() ,求AB边上的高CH。
,求AB边上的高CH。
分析 注意到![]() ,在
,在![]() 中,构造关于CH的方程。
中,构造关于CH的方程。
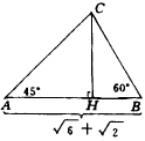
解:设![]() ,在
,在![]() 中,
中,![]() ,于是
,于是
![]() ,
,
所以有关于h的方程
![]() ,
,
解这个方程,得
![]() ,
,
∴![]() 。
。
点拨 这是一个利用三角函数建立方程的例题,是方程思想在解直角三角形中的应用。
在解直角三角形中,根式运算起着重要的作用。本例中关于![]() 的计算如果是这样:
的计算如果是这样:
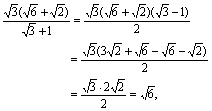
就不是好的计算过程,如果看到![]() 就有简便的算法
就有简便的算法
![]() 。
。