 设为首页
设为首页
 加入收藏
加入收藏
典型例题
例1 下列不等式成立的是( )
(A)![]()
(B)![]()
(C)![]()
(D)![]()
解:![]() 。
。
![]()
∴![]() 。
。
故应选D
说明:本题根据特殊角的三角函数值比较大小,进而选出正确答案。
例2 在Rt![]() 中,
中,![]() ,如果
,如果![]() ,则
,则![]() 等于( )
等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
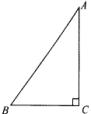
解:如图,在Rt![]() 中,设
中,设![]() ,则
,则![]() 。
。
![]()
说明:本题根据锐角三角函数的定义,利用“直接法”求解。
例3 求下列各式中的锐角x。
(1)![]() ;
;
(2)![]() 。
。
分析:综合考查换元思想,方程解法,特殊角的三角函数值;(1)由原方程得![]() ,把
,把![]() 看作一个量,从而列出
看作一个量,从而列出![]() ;(2)令
;(2)令![]() ,则原方程化为关于t的一元二次方程,把t求出来,然后再求x的值。
,则原方程化为关于t的一元二次方程,把t求出来,然后再求x的值。
解:(1)∵![]()
∴![]() ,
,
∴![]() 。
。
![]() 。
。
(2)令![]() ,原方程可化为:
,原方程可化为:
![]() 。
。
得:![]() ,
,
![]() 。
。
说明:换元思想可以化繁为简,化难为易,化未知为已知,是中学数学常用的数学方法,望读者仔细体会。
例4 在Rt![]() 中,
中,![]() ,垂足为
,垂足为![]() ,求AB的长和
,求AB的长和![]() 的值。
的值。
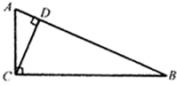
解:如图,
![]()
![]() ∽
∽![]() ,
,
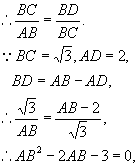
![]() 或
或![]() (舍去)。
(舍去)。
由勾股定理,得![]() 。
。
![]() 。
。
说明:利用三角形相似找出本题的解题思想,因此,对学过知识要灵活运用。
例5 已知![]() 为锐角,且
为锐角,且![]() ,
,
求:![]() 的值。
的值。
解:原式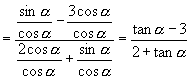 。
。
![]() ,
,
∴原式![]() 。
。
说明:本题的解法比较巧妙,也可以由![]() 得
得![]() ,即
,即![]() ,代入要求的式子,得
,代入要求的式子,得![]() 求解,方法较多,要找出一种较好的解法。
求解,方法较多,要找出一种较好的解法。
例6 在![]() 中,求证:
中,求证:![]() 。
。
证明:在![]() 中,
中,
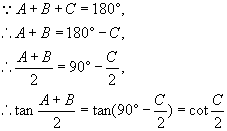
说明:等式![]() 成立是有条件的,即“在
成立是有条件的,即“在![]() 中”,如果把这个条件去掉,则等式不一定成立了。类似地还可以证明
中”,如果把这个条件去掉,则等式不一定成立了。类似地还可以证明
![]() 。
。
例7 在![]() 中,
中,![]() ,求:(1)
,求:(1)![]() 的值;(2)
的值;(2)![]() 的值。
的值。
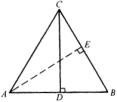
分析:为了求![]() 、
、![]() 的值,就要分别构造出以
的值,就要分别构造出以![]() 、
、![]() 为内角的直角三角形。
为内角的直角三角形。
解:(1)如图,过点A作![]() 于E,则
于E,则
![]() ,即
,即![]() ,
,
![]() ,
,
则 ![]() 。
。
∴![]() 。
。
在Rt![]() 中,
中,![]() 。
。
(2)由(1)知,![]() ,
,
则![]() 。
。
过点C作![]() 于D,
于D,
由![]() ,
,
得![]() ,
,
![]() 。
。
在Rt![]() 中,
中,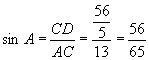 。
。
说明:锐角三角函数是在直角三角形内定义的,因此构造直角三角形就成为利用锐角三角函数解题的基本手段。