第八节 反比例函数及图象

典型例题

　　例1、已知一次函数 的图象与反比例函数 的图象相交，其中有一个交点的纵坐标为-4，求这两个函数的解析式．

　　解： 依题意，由两个函数解析式得

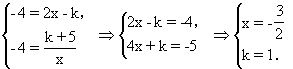
　　　所以一次函数和反比例函数的解析式分别为

　　注意：这是关于一次函数和反比例函数的综合题，解本题的关键是要抓住两图象交点这个主要矛盾，它既在一次函数图象上，又在反比例函数图象上，从而转化为解二元一次方程组，问题得以解决．

　　例2、 已知y=y₁+y₂，y₁与x+1成正比例，y₂与x²成反比例，并且x=-1时，y=1； 时， .求 时y的值.

　　

　　　

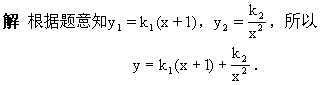
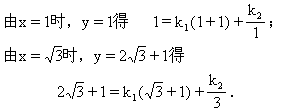
　　　解方程组

　　　

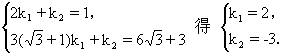
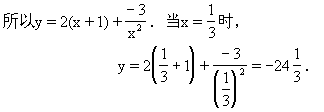
　　注意： 解本题的关键是正确理解什么叫y₁与x+1成正比例，y₂与x²成反比例，即把x+1与x²看成两个新的变量．

　　例3、已知反比例函数 的图象和一次函数 的图象都经过点P(m，2)．

　　(1)求这个一次函数的解析式；

　　(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上，顶点C、D在这个反比例函数的图象上，两底AD、BC与y轴平行，且A和B的横坐标分别为a和a+2，求a的值．

　　  解：（1）点 在函数 的图象上，所以 ，P点

　　　坐标为(6，2)．因为一次函数y=kx-7的图象经过点P(6，2)，所以

　　　

　　　

　　(2)因为点A、B的横坐标分别为a和a+2，由此可得

　　　

　　　

　　　

　　　

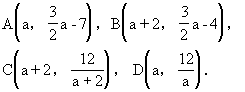
a=-4或a=2．

　　　经检验a=-4，a=2均为所求的值．

　　点评 本题是综合考察学生能力，培养数形结合的思想，点在曲线上则点的坐标应满足函数方程．另外要注意检验．

返回页首