第九节 由一个二元二次方程分式方程

典型例题

　　例1  解方程组

　　

　　分析：这是由两个二元二次方程组成的方程组，系数没有显著的特征，故我们思维的合理起点是设法把其中一个分解因式.

　　解：由（1），得

　　

　　∴  或

　　∴  原方程组可化为两个方程组：

　　

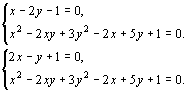
　　解之得原方程组的解为

　　

　　评注：此题解法是分解因式法.把其中的一个方程通过分解因式达到降次之目的，从而使原方程组转化为等价的两个方程组，可收化难为易的之功效.

　　例2  解方程组

　　

　　分析：两方程含x项的系数对应成比例，故可用消元法解之.

　　解：（1）－2·（2），得

　　

　　∴  或 .

　　原方程组可化为两个方程组

　　

　　

　　解之得原方程组的解为

　　

　　例3  解方程组

　　

　　分析：可将（2）化为 ，

　　则原方程组可化为

　　 或

　　解之，得

　　

返回页首