第七节 分式方程　

典型例题

　　例1  解方程.

　　解：原方程就是

　　去分母，得

　　整理后，得 

　　解这个方程，得

.

　　经检验，是增根，是原方程的根.

　　说明 去分母前的排列，变号（如本题中的变为），去分母时分母为1的整式或常数漏乘最简公母以及去括号时符号是否改变，都是解方程中容易出错的地方，解题过程中都要认真对待.

　　例2  解方程

　　解法一：原方程可化为

　　设，则原方程化为

，

　　去分母，得

，

　　解这个方程，得

.

　　当时，，

，

　　∴  此方程无实根.

　　当时，.

　　解这个方程，得

　　经检验，都是原方程的根.

　　解法二：去分母，整理，得

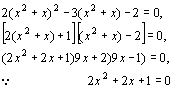
  或  .

　　方程的，无实数根.

　　∴    .

　　经检验，都是原方程的根.

　　点拨  从两种解法看到分式方程转化为整式方程的两种途径.解法一用的是换元法，因为，设，经过换元使方程得到化简.解法二用的是去分母，其后在解的过程中也是一种换元的思想，是把看成一个整体，当成一个未知数，只是没有显现出换元，如果换元方法掌握较好，对于这样的题采用解法二是否更为简捷些.

　　例3  当a取何值时，方程

　　去分母，得

　　解这个方程，得

　　∵  方程的解为负数，

　　∴  ，解得  .

　　，

　　∴  .  即  .

　　∴ 

　　∴  当且时，方程的解为负数.

　　点拨  分式方程的解必使是各分式的分母不等于零，在求适合某种条件的字母系数的值时，要特别注意这一点.

　　例4  某工厂计划生产480个零件，在实际生产中每小时多做了10个，结果不仅提前1小时完成任务，而且还比原计划多生产了10个零件.求原计划每小时做多少个零件？预计用多少时间？

　　分析  设原计划每小时做x个零件，那么预计用的时间就是小时，实际每小时生产了个零件，共计生产了个，所以实际所用的时间是小时.根据“实际比原计划提前1小时完成”这个等量关系列方程.

　　解：设原计划每小时做x个零件.

　　根据题意，有

.

　　去分母，整理，得

.

　　解这个方程，得

.

　　经检验，都是原方程的根，但生产零件的个数不能为负数，所以只取.

　　当时，.

　　答：原计划每小时生产60个零件，预计用8小时完成任务.

　　例5  甲、乙二人分别从相距27千米的A、B两地同时出发，相向而行，3小时相遇.相遇后两人各用原来速度继续前进，甲到达B地比乙到达A地早1小时21分.求两人的速度.

　　分析  本题中的主要等量关系是走完全程甲比乙少用1小时21分，可用等式表示.题目的前一句话中隐含了二人速度之间的关系，27千米的路程，二人用3小时相遇，就是说二人的速度和是每小时9千米，如果设甲每小时走x千米，那么乙每小时走（）千米.

　　解：设甲每小时走x千米，那么乙每小时走（）千米.

　　依题意，有

.

　　化简得

　　去分母，整理，得

　　解这个方程，得

　　经检验，都是原方程的根，但速度不能为负数，所以只取.

　　当时，.

　　答：甲每小时走5千米，乙每小时走4千米.

　　点拨  本题也可以把题中的两句话看成两个等量关系，列方程组求解.即

　　设甲的速度为每小时x千米，乙的速度为每小时y千米.

　　根据题意，有

.

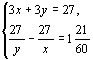　　方程组用代入消元法求解.

返回页首