第一节 比例线段

典型例题

　　例1  已知：线段 .求a、b、c的第四比例项.

　　分析：只要根据第四比例项的概念来求.

　　解答：由 ，可得 .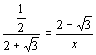

　　解得：

　　说明：要牢固掌握相关概念及性质.

　　例2  已知： ，求a、b的比例中项c.

　　分析：根据比例中项的概念来解.

　　解答：因为c为a、b的比例中项，所以 .所以 .

　　说明：容易把负值丢掉，应从概念上加以注意.

　　例2  已知： ，求 。

　　分析：只要根据比例的有关性质来解。

　　解答：由比例的基本性质，得： 。

　　所以 。

　　即 。

　　于是 。

　　说明：将比例式看成等式，用方程的观点处理比例式的问题是一种很好的方法。

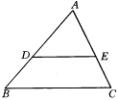
　　 例3  已知：如图所示，在 中， ，且 .（1）求AD的长；（2）求证： .

　　分析：（1）设AD为x，则已知的比例式是关于x的方程，（2）运用合比性质.

　　解答：（1）设 ，则 .

　　因为 ，

　　所以 ，

　　解之得 ，即 cm.

　　（2）因为 ，

　　所以 ，即 .

　　所以 .

　　说明：要根据情况灵活运用比例的性质.

　　例4  已知： ，求 .

　　分析：可分别从比的前后项凑出 、 .也可设比值为k，将x、y、z用k表示.

　　解答：解法一  因为 ，

　　所以 .

　　由等比定理，有 .

　　同样有 ，得 .

　　所以 .

　　解法二  设 ，则 .

　　所以 .

　　说明：比值法中引进的比值k，可以看成是辅助未知数，它在题目中为联系x、y、z的桥梁，这种方法我们常使用.

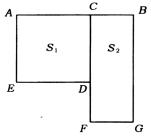
　　例5 如图，线段AB长 ，点C是黄金分割点， ，设以AC为边的正方形ACDF的面积为 ，以BC为一边，AB长为另一边的矩形BCFG的面积为 ，试求 和 .

　　分析 由黄金分割点的意义可知： ，设 ，可列出二次方程求出 ，则 均可求.

　　讲解 ∵点C是黄金分割点，

　　∴

　　设

　　解方程，得

　　∵线段不能为负，∴

　　∴

　　∴

　　

　　说明（1）当 ，这个结果要记住，当 时， .

　　（2）求得的 是显而易见的.∵点C是黄金分割点，∴ 即为 即为 .

返回页首