第九节 平行线等分线段定理

典型例题

　　例1 已知：如图， 中， 是 边上的中线， 是 的中点． 的延长线交 于点 ．求证： ．

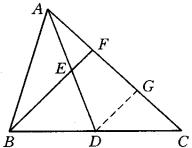
　　分析：要证 ，只要能在 上取一点 能证明 即可．

　　解答：过 点作 交 于点 .

　　因为 ， ，

　　所以 （经过三角形一边的中点与另一边平行的直线必平分第三边），

　　又因为 ， ，

　　所以 （经过三角形一边的中点与另一边平行的直线必平分第三边）．

　　于是 .

　　说明：已知三角形一边中点，常过该点作三角形其他边的平行线，构成平分第三边的基本图形，这是常用的添辅助线的方法。

　　例2 已知线段 ，求作：线段 上一点 ，使 .

　　分析：要求出点 使 ，关键是把线段 五等分．

　　解答：

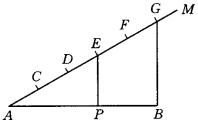
　　1．过 作射线 ；

　　2．在 上以任意长顺次截取 ；

　　3．连结 ，过 作 ，交 于 . 则 点为所求的点．

　　说明：要在已知线段 上求作一点 ，使 ，先要把 等分，再取其中 等分．

返回页首