 设为首页
设为首页
 加入收藏
加入收藏
典型例题
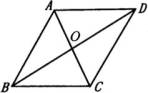 图1 |
【例1】如图1, ![]()
![]() 的对角线
的对角线![]() 、
、![]() 相交于
相交于![]() ,则图中全等三角形有( )
,则图中全等三角形有( )
A.2对 B.3对 C.4对 D.5对
【分析】由平行四边形的对边平行、对角线互相平分,可得全等三角形有:△![]() 和△
和△![]() ,△
,△![]() 和△
和△![]() ,△
,△![]() 和△
和△![]() 、△
、△![]() 和△
和△![]() .
.
【答案】C
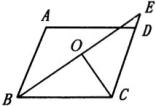 图2 |
【例2】如图2, ![]()
![]() 中,
中,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 和
和![]() 的延长线交于
的延长线交于![]() ,
,
求证:![]() .
.
【分析】证线段相等,可证线段所在三角形全等.可证△![]() ≌△
≌△![]() .已知
.已知![]() 为公共边,
为公共边,![]() ,又易证
,又易证![]() .问题得证.
.问题得证.
【证明】在 ![]()
![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
又∵![]() (角平分线定义).
(角平分线定义).
∴![]() ,
,
又∵![]() ,
,![]()
∴△![]() ≌△
≌△![]()
∴![]() .
.
说明:证线段相等通常有两种方法:(1)在同一三角形中证三角形等腰;(2)不在同一三角形则证两三角形全等.
本题也可根据等腰三角形“三线合一”性质证明结论.
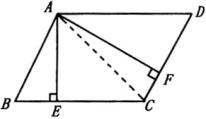 图3 图3 |
【例3】如图3,在 ![]()
![]() 中,
中,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的面积.
的面积.
【解】在 ![]()
![]() 中,
中,![]() ,
,![]() 、
、![]() .
.
在![]() △
△![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
在![]() △
△![]() 中,
中,![]() .
.
∴![]() .
.
故![]() .
.
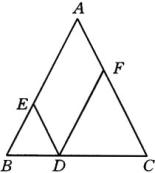 【例4】已知:如图,
【例4】已知:如图,![]() 是等腰△
是等腰△![]() 的底边
的底边![]() 上一点,
上一点,![]() ,
,![]() .求证:
.求证:![]() .
.
【分析】由于![]() ,
,![]() ,从而可以利用平行四边形的定义和性质,等腰三角形的判定和性质来证.
,从而可以利用平行四边形的定义和性质,等腰三角形的判定和性质来证.
【解】因为![]() ,
,![]() ,所以四边形
,所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]() .
.
所以![]() .
.
说明:证明一条线段等于另外两条线段的和常采用的方法是:把三条线段中较长的线段分为两段,证明这两段分别等于另两条线段.
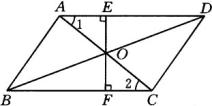
【例5】如图,已知: ![]()
![]() 中,
中,![]() 、
、![]() 相交于
相交于![]() 点,
点,![]() 于
于![]() ,
,![]() 于
于![]() ,求证:
,求证:![]() .
.
【分析】
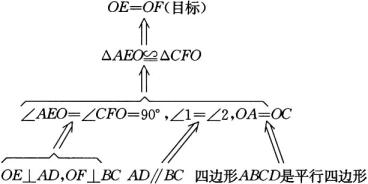
【解】因为四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,
,![]() .
.
又因为![]() 、
、![]() 交于
交于![]() 点,
点,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() .
.
于是△![]() ≌△
≌△![]() .
.
从而![]() .
.
说明:要学会用这种“倒着找”的方法进行分析.
此处不能写成“四边形![]() 是
是 ![]() ”.
”.
证明△![]() ≌△
≌△![]() 时,不能用条件“
时,不能用条件“![]() ”,这里并没有指明
”,这里并没有指明![]() 、
、![]() 、
、![]() 三点在一条直线上.
三点在一条直线上.
【例6】 已知:如图,![]() ,AC、BD交于O,且
,AC、BD交于O,且![]()
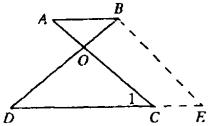 求证:
求证:![]()
证明:过B作![]() 交DC延长线于E,则
交DC延长线于E,则![]() 。
。
∵![]() ,
,![]() ,
,
∴![]()
∵![]() , ∴
, ∴ ![]()
∴![]() ∴
∴![]()
∴ ![]()
说明:本题条件中有“夹在两条平行线之间的相等且相交的线段”,由于位置交错而一时用不上,为此通过作平行线,由“夹在两条平行线间的平行线段相等”将线段AC平移到BE,得到等腰△BDE,使问题得解.
夹在两条平行线间的平行线段相等,是一个能简化证明过程的定理,因为由条件本身可得到一个平行四边形,因此当题目结论只需要证行四边形对边相等,而不需要平行四边形的其他性质时,可直接由上述定理得到线段相等.