第一节 四边形

典型例题

　　例1 如果四边形的四个内角度数比为1：2：3：4，那么这四个内角的度数分别为__________.

　　分析：根据四边形内角和定理知，四边形内角和为360°，依条件可设四个角的度数分别为x、2x、3x、4x，列方程求出K，可进一步求得这四个角的度数.

　　解：设这四个角的度数分别为x、2x、3x、4x，由四边形内角和360°，得：

　　　

　　例2  如图所示，四边形ABCD中， ，AE、CF分别平分 和 .求证： .

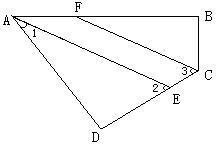
　　分析  欲证明 ，只需证明 ，由于 ，只需证 ，这就要联想到四边形的内角和定理.

　　证明 

　　

　　∵AE、CF分别平分 、 ，

　　 ，而 ，

　　

　　例3  求证：四边形的两条对角线之和大于它的周长的一半.

　　已知：如图所示，四边形ABCD中，对角线AC，BD相交于O.

　　求证：

　　

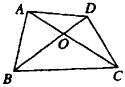
　　分析：两条对角线AC、BD将四边形ABCD分成了四个三角形△OAB、△OBC、△OCD、△ODA，在这四个三角形中分别利用两边之和大于第三边的定理即可得出需证的结论.

　　证明：在△OAB中， 　　 ①

　　在△OBC中， 　　　　　②

　　在△OCD中， 　　　　　③

　　在△ODA中， 　　　　　④

　　①＋②＋③＋④，得

　　

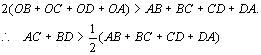
　　点拨：在解四边形的问题时，通常要将四边形的问题转化成三角形问题来解决.本例中观察到两条对角线将四边形分成四个三角形是解题的关键.

　　例4 长为3、5、6、15的四条线段能否构成一个四边形.

　　

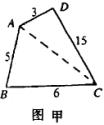
　　解：若能构成一个四边形

　　（1）若各边长如图甲中所示.连结AC.在△ADC中，由 ，得 ；在△ABC中，由 ，得 ，矛盾.

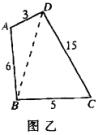
　　（2）若各边长如图乙中所示.连结BD.在△BDC中，由 ，得 ；在△ABD中，由 ，得 ，矛盾.

　　综上可知，长为3、5、6、15的四条线段不能构成一个四边形.

　　点拨：本题中连结AC、BD的目的是将四边形的问题转化为三角形的问题去解决.

返回页首