第十四节 线段的垂直平分线

典型例题

　　例1　如图，△ABC中，∠C＝ ，∠A＝ ，AB的在垂线交AC于D，交AB于E

　　求证：AC＝3CD

　　分析：要证AC＝3CD，即证AD＝2CD. 因AD与CD在一条直线上，因此解题受阻. 但观察条件发现：DE垂直平分AB，得AD＝BD，故有了新解题方向：只要能证明BD＝2CD即CD＝ BD即可. 这可由Rt△BCD含 角的性质而获得，至此解题路线已趋明朗.

　　证明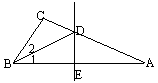：∵DE垂直平分AB

　　　∴AD＝BD

　　　∴∠1＝∠A＝

　　　∵

　　　∴∠2＝

　　　∴CD＝ BD

　　　∴CD＝ AD

　　　∴AD＝2CD

　　　即AC＝3CD

　　说明：当执果索因感到困难时，先由题目所给的条件入手，得到常见的结论，然后分析所得的结论与未知的关系.

　　例2. 在△ABC中，AB＝AC，AB的中垂直线与AC所在直线相交所得的锐角为 ，求底角B的大小.

　　分析：利用线段的垂直平分线的性质定理，等腰三角形的性质，三角形的内角和定理

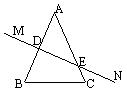
　　解：（1）当AB的中垂线MN与AC相交时，如图（1），

　　　∵∠ADE＝ ，∠AED＝

　　　∴∠A＝ －∠AED＝ － ＝

　　　∵AB＝AC　∴∠B＝∠C

　　　∴∠B＝

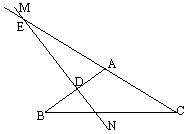
　　（2）当的中垂线与的延长线相交时，如图（2）

　　　∵∠ADE＝ ，∠AED＝

　　　∴∠BAE＝ －∠AED＝ － ＝

　　　∵AB＝AC　∴∠B＝∠C

　　　∴∠B＝

　　说明：做这类题关键是当图形未给定时，要画出所有符合条件的图形，并加以解答.

　　例3 （1）在△ABC中，AB＝AC，AB的垂直平分线交AB于N，交BC的延长线于M，∠A＝ ，求∠NMB的大小

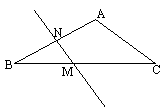
　　（2）如果将（1）中∠A的度数改为 ，其余条件不变，再求∠NMB的大小

　　（3）你发现有什么样的规律性？试证明之.

　　（4）将（1）中的∠A改为钝角，对这个问题规律性的认识是否需要加以修改

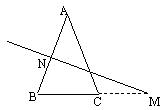
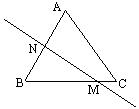
　　分析： 要想求角，应紧紧抓住中垂线的性质

　　解：（1）∵AB＝AC

　　　∴∠B＝∠ACB

　　　∴∠B＝

　　　∵∠BNM＝

　　　∴

　　（2）如图，同（1）同理求得

　　（3）如图，∠NMB的大小为∠A的一半

　　说明：这是由特殊到一般发现并证明比较明显的规律性的一次模拟，由（1）和（2）不难以感性上认识到∠BMN的大小是∠A的一半，但也容易以为点M一定在BC的延长线上，通过（4），也就是让△ABC保持AB＝AC的前提下，发生较大的变化，认识就更全面、更准确了。

返回页首