第十二节 等腰三角形的性质

典型例题

　　

　　分析：注意到题中所给的条件AB＝AC，得到三角形为等腰三角形。利用等腰三角形的性质对问题（1）可得 ；对问题（2）考虑到所给这个角可能是顶角也可能是底角；对问题（3）由三角形内角和为 可得此等腰三角形的顶角只能为 这一种情况。

　　略解：（1） （2）另外两内角分别为： （3）

　　说明：通过题目中的（2）、（3）渗透分类思想，训练思维的严密性。

　　例2．已知：如图，在 中，AB=AC， 于D，求证： .

　　分析：欲证角之间的倍半关系，结合题意、图形，观察已知角、边间的特殊性. 是等腰三角形的顶角，因此较容易找到它的半角. 从而转化为两角间的相等关系.

　　 证明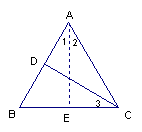：过点A作 于E.
　　　  
　　　 　 ，
　　　 　 　即

　　小结：作等腰三角形底边高线的目的是利用等腰三角形的三线合一性质，构造角的倍半关系，因此添加底边的高是一条常用的辅助线.

　　例3　已知：如图，D是等边△ABC内一点，DB＝DA，BP＝AB， DBP＝ DBC

　　求证： P＝

　　分析：要求出 P的度数，直接求出较难，根据已知AB＝BP＝BC，BD为公共边，

　　 DBP＝ DBC，所以，△BPD≌△BCD，因此考虑连结CD，因此可将 P转化成与之对应的等角 BCD，将求 P的度数变成求 BCD的度数，由已知易证△BPD≌△ADC，于是 BCD＝ ACD＝ C＝ ，得 P＝

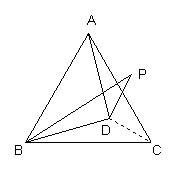　　证明：连结OC

　　　在△BPD和△BCD中

　　　

　　　

　　　在△ADC和△BCD中

　　　     

　　　

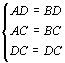
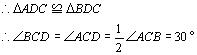
　　　因此， P＝

　　说明：本题证明的关键是辅助线CD，利用三角形全等得到 P的等角。

　　例4　求证：等腰三角形两腰上中线的交点到底边两端点的距离相等

　　分析：按解文字证明题的三个步骤：（1）画图；（2）写出已知，求证；（3）书写证明过程分别进行。

　　已知：如图，AB＝AC，BD、CE分别为AC边、AB边的中线，它们相交于F点

　　求证：BF＝CF

　　分析：为证等量，考虑全等，即可先证△ABD≌△ACE得 1＝ 2，再证△BEF≌△CDF

　　证明：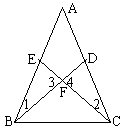

　　　∵BD、CE是△ABC的两条中线，AB＝AC

　　　∴AD＝AE，BE＝CD
　　　在△ABD和△ACE中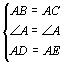
　　　∴△ABD≌△ACE

　　　∴ 1＝ 2
　　　在△BEF和△CED中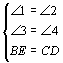
　　　∴△BEF≌△CED

　　　∴BF＝FC

　　说明：此题为文字证明题，首先做好转化工作，文字语言图形化、图形语言式子化，即依题意画出恰当的几何图形，再写出已知、求证，注意画图要具有代表性，切忌以特殊代替一般，而几何语言要精练，能用几何式子表达的不要用文字语言，最后再在认真分析做题思路的基础上，写出证明过程。

返回页首