第十节 基本作图　

典型例题

　　1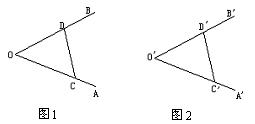．作一个角等于已知角

　　分析：解作图题的方法与证明题解法不相同，它一般应包括已知，求作。对于作图首先将文字叙述转化为数学语言，即要写出题目的已知、求作、作法、证明。

　　已知：AOB

　　求作： 使 ＝ AOB

　　作法：1、作射线

　　2、以点O为圆心，以任意长为半径作弧，交OA于C，交OB于D

　　3、以点 为圆心，以OC长为半径作弧，交 于

　　4、以点 为圆心，以CD长为半径作弧，交前弧于

　　5、经过点 作射线 。 就是所求的角

　　证明：连结CD、C'D'，由作法可知

　　△C'O'D≌△COD(SSS)

　　∴∠C'O'D'=∠COD(全等三角形对应角相等)．

　　即∠A'O'B'=∠AOB．

　　说明：作图题的证明，常以作法为根据，只要“作法”中写明了作的是什么，证明中就可以用它作根据去证明．注意，在作图题的“证明”中，一般过程都写得比较简单．如这个证明三角形全等的地方，把条件省略了．

　　2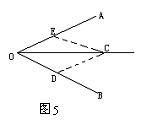．平分已知角

　　已知：∠AOB如图5

　　求作：射线OC，使∠AOC=∠BOC．

　　作法：(1)在OA和OB上，分别截取OD、OE，使OD=OE．

　　（2）分别以D、E为圆心，大于 的长为半径作弧，在 内，两弧交于点C．

　　(3)作射线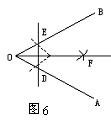OC．

　　OC就是所求的射线．

　　证明：连结CD、CE，由作法可知

　　△ODC≌△OEC(SSS)

　　∴　 ∠COD=∠COE(全等三角形的对应角相等)．

　　即∠AOC=∠BOC．

　　小结：

　　(1)基本作图1、2有一个不同之点，即基本作图2要把射线OC作在∠AOB内部，位置有指定性，基本作图1所作的∠A'O'B'并不受∠AOB的位置限制，但通常把∠A'O'B'作在∠AOB的近旁．

　　(2)作图工具只限直尺和圆规，用铅笔画图，并保留作图过程中的辅助线(作图痕迹)．

　　(3)只画图的题，要求画完图，写明所求作的图形．如基本作图中要写出“∠A'O'B'就是所求的角．”

　　3．经过一点作已知直线的垂线

　　分两种情况来考虑：

　　(1)经过已知直线上的一点作这条直线的垂线．

　　(2)经过已知直线外的一点作这条直线的垂线．

　　分析：如果我们把D、E看成一条直线上的两点，那么点O就是这条直线外的一点，图6启发我们经过直线DE外一点O作这条直线的垂线的关键在于确定点F.

　　①已知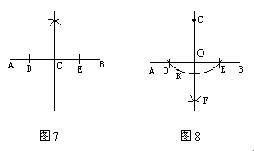：直线AB和AB上一点C，如图7．

　　求作：AB的垂线，使它经过点C．

　　作法：作平角ACB的平分线CF直线CF就是所求的垂线。

　　证明：由作法可知，

　　

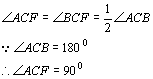
　　即CF是AB的垂线。

　　②已知：直线AB和AB外一点C，如图8．

　　求作：AB的垂线，使它经过点C．

　　作法：1、任意取一点K，使K和C在AB的两旁

　　2、以C为圆心，CK长为半径作弧，交AB于点D和E

　　3、分别以D和E为圆心，大于 DE的长为半径作弧，两弧交于点F

　　4、作直线CF

　　直线CF就是所求的垂线

　　证明：提示：连结CD、CE、FD、FE，设CF与AB交于点O．首先证明△CDF≌△CEF，再证明△CDO≌△CEO或△FDO≌△FEO，从而得∠DOF=∠EOF=90°．

　　说明：几何语言要准确，严密、规范

　　4．作线段的垂直平分线

　　已知：线段AB

　　求作：线段AB的垂直平分线。

　　分析：注意题目有两个条件，(1)垂直，（2）平分

　　作法：（1）分别以点A和B为圆心，大于 的长为半径的弧，两弧相交与点C和D.

　　(2)作直线CD；

　　直线CD就是线段AB的垂直平分线。

　　例5、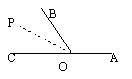如图，已知钝角 ，求作 的补角的一半。

　　分析：本题的实质是先作出 的补角，再作这个补角的平分线。

　　作法：（1）作OA的反向延长线OC；

　　（2）作 的平分线，则 ， 就是所求得角。

　　例6、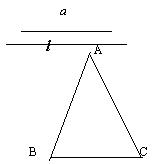已知：线段 ；求作： ，使

　　作法：1、作线段BC＝a

　　2、分别以点B、C为圆心，以 为半径作弧，两弧交于点A

　　3、连结AB、AC

　　 就是所求作的三角形

　　例7、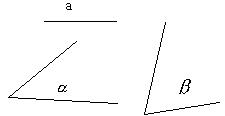已知两角和其中一角的对边，求作三角形

　　已知： ，求作：

　　作法：1、作线段

　　2、在BC的同侧作 DE、EC交于点A。

　　 为所求的三角形

　　证明：（略）

返回页首