第二节 三角形三条边的关系

典型例题

　　

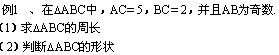
　　分析：在已知三角形的两边为 时，则第三边 的取值范围为：

　　 特别注意用“两边之差小于第三边”时，一定用较大的边减去小的边，
在不知谁大时，为了保证两边的差非负，需加绝对值.

　　解：（1）根据三角形三边关系有

　　　　

　　（2）（略）

　　说明：解本题的关键是根据三角形三边关系定理及推论并结合题设条件列出不等式组.

　　例2　草原上有4口油井，位于四边形ABCD的4个顶点，如图1现在要建一个维修站H，试问H建在何处，才能使它到4口油井的距离HA+HB+HC+HD为最小，说明理由.

　　分析：此题是一个实际问题，首先应转化为数学问题，即转化为三角形，再利用三角形三边关系定理求解.

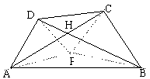
　　解：维修站应建在两条对角线的交点H处

理由如下：

　　取不同于H的点P，三角形的两边　之和大于第三边有：

　　 PD+PB＞HD+HB　　PC+PA＞HC+HA

　　 所以：PD+PB+PC+PA＞HD+HC+HB+HA

　　 即HD+HC+HB+HA为最小.

　　说明：此题是一道典型问题――求线段之和最值问题，首先要找到符合条件的点，然后推理说明理由.所应用的解决方法也是常见的方法，需要添加辅助线，构成新的三角形，然后运用三角形三边关系定理.

返回页首