第五节 含有字母系数的一元一次方程

典型例题

含有字母系数的一元一次方程

　　例１、解关于 的方程：

　　（1） ；

　　（2） ；

　　（3） ．

　　分析：解这类问题的关键是分清已知数和未知数，然后按照解法步骤进行解答．第（1）题中， 、 是已知数，并注意到条件 和 ，方程两边都乘以 ，约去分母；第（2）题中， 是已知数，方程两边都乘以2，把 移到方程左边，与 合并；第（3）题中， 是已知数， ，方程两边都乘以 ，约去分母．

　　解：（1）方程两边都乘以 ，得

　　　 ，

　　　合并同类项，得 ．

　　　∵ ，∴ ．

　　方程两边都除以   得 ．

　　（2）方程两边都乘以2，得

　　　 ，

　　　移项得 ，

　　　合并同类项得 ．

　　　∵ ，∴ ．

　　　系数化为1得 ．

　　　即 ．

　　（3）方程两边都乘以 ，约去分母，得

　　　 ，

　　　去括号得 ，

　　　整理得 ．

　　　∵ ，∴ ．

　　　系数化为1得 ．

　　小结：含字母系数的一元一次方程求解中首先要分清已知数和未知数，在将未知数系数化为1的过程中，要考虑到方的同解原理的要求，等式两边同乘同除同一个数一定要保证是非0数。最终结果应是最简分式或整式，同时要检验。

　　例2、在公式 中，（1）已知 、 和 ，求 ；（2）已知 、 和 ，求 ．（所有字母均不为零）

　　分析：公式变形的实质是解关于字母系数的一元一次方程．第（1）题中 、 和 是已知数， 是未知数；第（2）题中 、 和 是已知数， 是未知数．

　　解：（1） ．

　　　　∵ ，

　　　　∴方程两边同时除以 ，得

　　　　　 ，

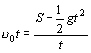　　　即　 ．

　　（2）移项得 ．

　　　∵ ，∴ ．

　　　系数化为1，得

　　　 ，

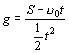　　　即　

　　小结：公式变形中首先要分清几个量那些是已知数，那个是未知数，严格遵循法则和解题步骤求解。公式变形的实质是几个量间关系的几种表现形式。

　　例3、解下列关于x的方程：

　　（1）

　　（2）

　　分析：这组题仍是解含有字母系数的一元一次方程，所不同的是没有给出字母应满足的条件，也就是将方程变形成 后，a没有限制，即可以为0，所以需分类讨论。

　　解：（1）若 ，则

　　若 ，这时

　　方程变为：

　　方程的解为任意数。

　　（2）去括号，得

　　移项、合并，得

　　若 时，方程的解是 ；

　　若 ，则方程变为 ，方程的解为任意数；

　　若 ，则方程变为 ，方程无解。

　　小结：含字母系数的一元一次方程求解中若对已知数没有条件限制，则需要讨论求解，讨论时一定要全面，保证不多不漏，解是已知数不同取值时不同情况。此题对于学有余力的学生课后研究。

返回页首