第四节 分式的加减法

典型例题

　　例1、通分 ， ， 。

　　分析：分母系数的最小公倍数是48，字母因式m，n的最高次数幂分别为 ， ，所以最简公分母是 。

　　解： 最简公分母是

　　  

　　

　　

　　小结：通分是分式加减法运算的基础，不同分母的分式相加减，必须先通分，分式的通分关键是找出最简公分母。

　　例2、通分 ，

　　分析：分式的分母是多项式，要找最简公分母，首先把各分母分解因式。

　　解： ，

　　 最简公分母是：

　　

　　

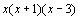
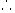
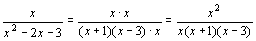
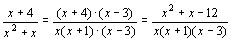
　　小结：，对于分母式多项式的分式通分，首先要因式分解，找出所有的因式。

　　例3、计算：（1） ； （2） ．

　　分析：两题都是最新中考题．由于分式运算可综合考查许多知识点，所以是一个命题热点．在做分式计算时，要做到：牢记法则，顺序计算，善用技巧，认真细心．如：第（1）题先通分后约分；第（2）题混合运算，先算括号内的，再将除法变为乘法，最后约分．

　　解：（1）原式

　　              ；

　　     （2）原式

　　              

　　              ．

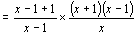
　　小结：分式的加减法首先要找到最简公分母，对于分母时多项式的先因式分解，整式或常数看作分母1的分式，步骤要完整，不要跨越步骤。

　　例4、化简 ．

　　分析：这是一道分式的四则混合运算题，若按顺序计算，一般应先算括号内的，再将除法变为乘法，最后约分．本题可先因式分解、约分、求出小括号内的结果并化简，然后再进行除法运算．

　　解：原式

　　         

　　         

　　         

　　小结：分式的四则运算注意运算的顺序，按部就班的求解，由涉及的知识较多，计算过程较繁，出错的可能性较大，一定要熟练掌握前面的知识，运算细心仔细。

　　例5、锅炉房储存了 天用的煤 ，要使储存的煤比预定的多用 天，每天应该节约用煤多少？

　　分析：本题是有关分式的知识在实际中的应用．原计算 天用煤 ，则原计划一天用煤 ；现改为要求 天用 ，则现在每天用煤 ，即每天应节约用煤 ．

　　解：每天应节约用煤 ．

　　答：每天应该节约用煤 ．

　　例6：先化简，再求值： ．其中 、 满足方程组 ．

　　分析：化简求值是一种常见题型．它可以综合考查分式的运算和数的运算，一般先化简再求值．按照题中指明的运算顺序，应先将前两个分式分解因式、约分化简，同时将括号内通分，注意整数“2”看作分母为1，转化为同分母分式相加，再将分子相加．注意不必先求方程组的解，而应将化简原式的结果适当结合，进行整体代入，减少计算量．

　　解：原式

　　         

　　          ．

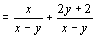
　　∵ 、 满足 ，

　　∴原式 ．

　　小结：（1）在分式化简求值问题中要根据分式的特点，灵活的运用运算法则，确定正确的顺序，规范解题过程；（2）整体代入思想在数学计算中应用很多，具体运用时要把握好，达到简便计算的目的。

返回页首