第十节 定理与证明

典型例题

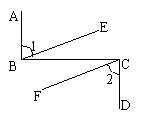　　 例1  已知：如图AB⊥BC，BC⊥CD且∠1=∠2，求证：BE∥CF

　　证明：∵AB⊥BC，BC⊥CD（已知）

　　∴_____=_____=90°（　）

　　∵∠1=∠2（已知）

　　∴_____=_____（等式性质）

　　∴BE∥CF（ ）

　　答案：∠ABC=∠BCD，垂直定义，∠EBC=∠BCF，内错角相等，两直线平行．

　　说明：了解证明的结构，和逻辑关系．

　　例2  已知：如图，EF⊥AC，BC⊥AC，∠1=∠B，求证：AD∥EF．

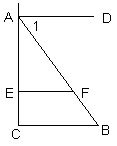　　 分析：由EF⊥AC，BC⊥AC，可推出EF∥CB，又由∠1=∠B，可推出AD∥CB，从而又可推出AD∥EF．

　　证明：∵EF⊥AC，BC⊥AC （已知），

　　∴EF∥CB（垂直于同一直线的两直线平行）．

　　∵∠1=∠B（已知)．

　　∴AD∥CB （内错角相等两直线平行)．

　　∴AD∥EF（平行于同一直线的两直线平行）．

　　说明：在证明中可以清楚地看出证明的结构，这里“∵EF⊥AC，BC⊥AC （已知）， ∴EF∥CB（垂直于同一直线的两直线平行）．”与“∵∠1=∠B（已知)． ∴AD∥CB （内错角相等两直线平行)．”的先后次序可以交换．

　　例3  已知：如图，AD∥BC，AD平分∠EAC．

　　求证：∠B＝∠C．

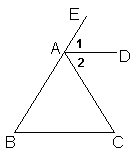　　 分析：由AD∥BC可推出∠1=∠B，∠2=∠C，又AD平分∠EAC，于是可推出∠1=∠2，通过等量代换即可推出∠B＝∠C．

　　证明：∵AD∥BC（已知），

　　∴∠1=∠B（两直线平行，同位角相等），

　　∠2=∠C （两直线平行，内错角相等）．

　　∵AD平分∠EAC（已知），

　　∴∠1=∠2（角平分线定义）．

　　∴∠B＝∠C（等量代换）．

　　说明：由已知AD∥BC可同时推出两个结论，∠1=∠B和∠2＝∠C，其推论过程是：

　　∵AD∥BC，

　　∴∠1=∠B．

　　∵AD∥BC，

　　∴∠2＝∠C．

　　为简便起见，可书写为：

　　∵AD∥BC， 

　　∴∠1=∠B，∠2＝∠C．

　　但要注意不要书写为：

　　∵AD∥BC，

　　∴∠1=∠B．

　　∴∠2＝∠C．

　　因为这将造成“∠2＝∠C”是由“∠1=∠B”推出的错误推理，其实，上述没有因果关系．

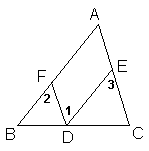
　　例4   已知：如图，点D、E、F分别在BC、AC和AB上，DF∥AC，∠1＝∠A．

　　求证；AB∥DE．

　　分析：欲证AB∥DE，首先要观察图形，看AB和DE被哪一条直线所截，图中AB和DE即被DF所截，同时又被AC所截，这时可任取其中一种情况，若取AB和DE被DF所截，只须证∠l＝∠2即可；若取AB和DE被AC所截，只须证∠3＝∠A即可．注意到已知条件EF∥AC，可以推出∠l＝∠3，∠2＝∠A，再加上之∠1＝∠A，这个已知条件，两种证法都不难实现．

　　证1：∵DF∥AC（已知），

　　 ∴∠2＝∠A（两直线平行，同位角相等），

　　∵∠1＝∠A（已知）

　　∴∠l＝∠2（等量代换）．

　　∴AB∥DE（内错角相等，两直线平行）．

　　证2：∵DF∥AC（已知），

　　∴∠1＝∠2（两直线平行，内错角相等），

　　∵∠1＝∠A（已知）

　　∴∠3＝∠A（等量代换）．

　　∴AB∥DE（同位角相等，两直线平行）．

　　说明：用综合分析法探求证明思路时，一般可先从求证结论出发，分析欲推出此结论需要什么条件?此时，这样的条件可能不止一个，可选定其中一个，然后再从已知条件出发，以此条件为目标推出已知条件，这个条件一旦推出，证明思路即告形成．

　　例5  如图，已知AD⊥BC，EF⊥BC，∠1＝∠E．

　　求证：AD为∠BAC的平分线．

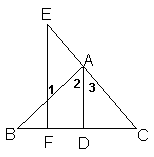　　 分析：要证AD为∠BAC的平分线，即证∠2＝∠3，由AD⊥BC，EF⊥BC，可推得AD∥BC．所以有∠2＝∠1，∠3＝∠E，又已知∠1＝∠E，由等量代换就可以得∠2＝∠3．

　　证明：∵AD⊥BC，EF⊥BC（已知）

　　∴AD∥BC （垂直于同一直线的两直线平行）

　　∴∠l＝∠2（两直线平行，内错角相等）

　　  ∠3＝∠E（两直线平行，同位角相等）

　　又∵ ∠1＝∠2（已知）

　　∴∠2＝∠3（等量代换）

　　∴AD为∠BAC的平分线（角平分线的定义）．

　　说明：（3）分析是证题的关键，在分析时要紧紧抓住要征的结论(即目标)，追溯能导致结论成立的条件，一步一步追溯下去，一直到这些条件都己具备为止．这时，证题思路已经基本形成．证明过程要从“已知”说起，最后推导出结论的成立．

　　（2）“∴AD∥BC （垂直于同一直线的两直线平行）”与“∴∠l＝∠2（两直线平行，内错角相等）， ∠3＝∠E（两直线平行，同位角相等）”的位置是不能交换的，因为后者是由前者推理得到的．

　　（3）把“∵ ∠1＝∠2（已知）”与

　　“∵AD⊥BC，EF⊥BC（已知）

　　∴AD∥BC （垂直于同一直线的两直线平行）

　　∴∠l＝∠2（两直线平行，内错角相等）

　　  ∠3＝∠E（两直线平行，同位角相等）”

　　可以交换，但这样因为条件与结论相距较远，不利于推理．

　　例6  求证：如果一条直线和两条平行线中的一条垂直，那么这条直线和另一条垂直．

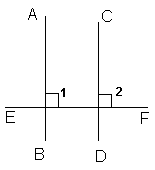
　　分析：(1)根据命题画出图形，先画出两条平行线AB、CD，再画出一条直线EF与AB垂直．(如图)

　　(2)分清命题的题设和结论，题设是：一条直线和两条平行线中的一条垂直．结论是：这条直线也和另一条垂直，再根据题设和结论写出已知事项和求证事项．

　　 (3)正确地写出推理过程．

　　已知：如图，AB∥CD，EF⊥AB，求证：EF⊥CD．

　　证明：∵AB∥CD  (已知)，

　　∴∠1＝∠2  (两直线平行，同位角相等)．

　　∵EF⊥AB   (巳知)，

　　∴∠1=90°  (垂直定义)，

　　∴∠2＝90° (等量代换)．

　　∴EF⊥CD  (垂直定义)

　　说明：对于一个命题的证明，第一步结合题意，画出图形，这是非常重要的一步，对题意不理解，或者把图形画错了，下面两步就无法进行，第二步的关键是分清命题的题设和结论，命题的题设是已知事项，命题的结论是求证事项，第三步是分析证明命题的途径，正确地写出证明过程．

返回页首