第六节 角的度量

典型例题

　　例1：将下列各题化成度、分、秒的形式．

　　（1）45．6°（2）78．43°（3）35．564°

　　解:(1)因为45.6°=45°+0.6°,又因0.6°=60′×0.6=36′,所以45.6°=45°36′．

　　(2)因为78.43°＝78°＋0.43°，又因为0.43°=60′×0.43=25.8′，0.8′=60′×0.8=48″，

　　　所以78.43°=78°25′48″．

　　(3)∵35.564°=35°＋0.564°，

　　　又∵0.564°=60′×0.564=33.84′，0.84′=60″×0.84=50.4″≈50″．

　　　∴35.564°≈35°33′50″．

　　说明：在解题过程中，要提醒学生注意以下几点：

　　（1）此题的类型是大单位化小单位，整个过程用乘法．

　　（2）第（1）题将0.6°化成36′，不再有秒．第（2）题将0.43°化成25.8′后，0.8′还要再化成秒．第（3）题将0.564°化成33.84′后，0.84′化成50.4″，但秒下面不再有更小的单位，所以对0.4″进行四舍五入．这三道题对三种情况进行了讨论，学生在做题过程中，要根据不同情况，考虑是再向更小的单位换算还是进行四舍五入．

　　例2 计算：

　　(1)32°19′+16°53′16″

　　(2)180°-126°43′12″

　　分析：进行加法运算时，先算秒，再算分，最后算度， 够60″时，把60″化为1′，够60′时，把60′化为 1°．进行减法运算时，不够减，借1°化为60′．

　　解：(1)19′+53′=72′=1°12′

　　　∴32°19′+16°53′16″=49°12′16″

　　(2)180°-126°43′12″=179°59′60″-126°43′12″=53°16′48″

　　说明：借1°化为60′，借1′化为60″，所以180°=179°60′=179°59′60″．

　　例3：若∠AOB=∠170°，∠AOC=7O°∠BOD=60°，求：∠COD的度数．

　　分析：题设中未给图形，应将图形的各种情况都考虑到．

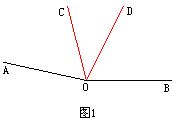
　　解：如图1，∠COD=∠AOB-∠AOC-∠BOD=170°-70°-60°=40°

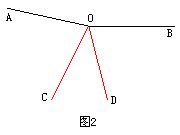
　　如图2，∠COD=360°-∠AOB-∠AOC-∠BOD=360°-170°-70°-60°=60°

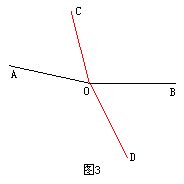
　　如图3，∠COD=∠AOB-∠AOC+∠BOD=170°-70°+60°=160°

　　如图4，∠COD=∠AOB+∠AOC-∠BOD=170°+70°-60°=180°

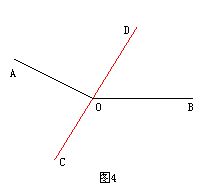
　　说明：本例中由于∠AOC的一边OC和∠BOD的一边OD的位置不同，(1)OC和OD都在∠AOB的内部，(2)OC和OD都在∠AOB的外部，(3)OC和OD一条在∠AOB的内部，另一条在∠AOB的外部，分为四种不同情况，求出∠COD的不同度数．

返回页首