第八节 同底数幂的除法

典型例题

　　例1 计算

　　（1）

　　（2）

　　（3）

　　（4）

　　分析  此例都可用同底数幂的除法的性质进行计算，注意运算符号，算出最终结果，如 和 都能继续计算.

　　解：（1）

　　（2）

　　（3）

　　（4）

　　例2 判断下列各式是否正确，错误请改正.

　　（1）

　　（2）

　　（3）

　　（4）

　　（5）

　　解：（1）不正确，应改为 ，法则中底数不变，指数相减，而不是指数相除.

　　（2）不正确，应改为 ， 与 底数不同，要先化同底，即 再计算.

　　（3）不正确，应改为 ， 与 互为相反数，先化同底便可计算.

　　（4）不正确，应改为 ，指数相减应为 .

　　（5）正确.

　　例3 计算

　　（1）

　　（2）

　　分析   利用 ， （ ， 为正整数）来解题，并注意混合运算的顺序.

　　解：（1）

　　　

　　　

　　　

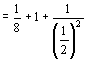
　　（2）

　　　

　　　

　　　

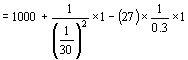
　　说明 负整数指数幂的计算，如底数是分数时，则将性质推广为(为正整数，)，会给分数计算带来方便.如：

　　 ，

　　例4   用科学记数法表示下列各数，并保留两个有效数字.

　　（1） 　　（2）

　　分析   先用科学记数法记数，再四舍五入求近似数，指数的确定：指数的绝对值等于第一个非零数字前的零的个数，这里包括整数位上的零，指数的符号是负.

　　解：（1）

　　（2）

　　说明  本例只讨论 小于1的数的表示方法.

　　例5  计算

　　（1）

　　（2）

　　分析 本例是包含多种运算的算式，要按照先乘方、再乘除、后加减的顺序运算，乘除法是同级运算，按顺序计算就可以.

　　解：（1）

　　　

　　　

　　　

　　　

　　（2）

　　　

　　　

　　　

　　说明  （2）题结果不能写成 ，应化简为 才行.

　　例6 计算（1）

　　（2）

　　分析 （1）题中的两个幂底数不同，一个是16，另一个是4，但 ，因此可将底数化为4，（2）题处理符号上要细心.

　　解：（1）

　　　

　　　

　　　

　　　

　　（2）

　　说明  底数不同的情况下不能运用同底数幂的除法法则计算.

　　例7 已知 ， ，求 . 

　　分析   ，将 、 整体代入便可.

　　解：

　　说明  本例逆用同底数幂的除法法则，不能误以为 .

返回页首