第三节 一元一次不等式和它的解法

典型例题

　　例1 解下列不等式，并把它的解集在数轴上表示出来：

　　（1）

　　（2）

　　解：（1）去分母，得 

　 　去括号，得 

　 　移项，得 

　 　合并同类项，得 

　 　系数化为1，得 

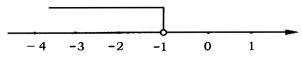
　　（2）由原不等式，得

　 　

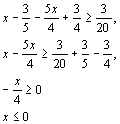
　　例2 解不等式：

　　

　　解：去分母，得

　 　

　 　去括号，得

　 　移项，得 

　 　合并同类项，得

　 　事实上

　 　∴ 原不等式无解．

　　说明：本题按一元一次不等式的解题步骤，最后得到，而，从而推出，与0小于一切正数相矛盾．所以，原不等式无解．

　　例3 解不等式

　　

　　解：去分母，得

　 　

　 　去括号，得

　 　移项，得

　 　

　 　∵ 不论 取任何有理数， 都为零

　 　而 

　 　∴ 可以取一切有理数．

　　例4 求不等式 的正整数解．

　　解：去分母，得

　 　去括号，得

　 　移项，合并同类项，得

　 　系数化为1，得

　 　依题意，其正整数解为1，2．

　　说明：本题是带有附加条件的不等式，这时可先求不等式的解集，然后从中找出满足条件的解．

返回页首