第二节 不等式的解集

典型例题

　　例1 判断下列说法是否正确？为什么？

　　（1） 是不等式 的解；

　　（2） 是不等式 的解集；

　　（3）不等式 的解集为 ；

　　（4）不等式 的解集为

　　解：（1）正确．因为1能使不等式 成立．

　　（2）不正确．因为不等式 有无数个解，而 仅是其中的一个，因此不能称为解集．

　　（3）不正确．因为小于1的数是不等式 的解，但是大于1小于3的数（如2，2．5等）也是不等式的解，因此 ，并不是不等式的所有解，因此不是不等式 的解集．

　　（4）正确，因为 是不等式 的所有解组成的集合．

　　说明：要注意区分“不等式的解”与“不等式解集”的意义．

　　例2 将下列不等式的解集在数轴上表示出来：

　　（1） ；　（2） ；　（3） ；

　　（4） ；　（5） ；　（6） （ ）

　　解：（1）如图1　　　　　　　　（2）如图2

　
图1　　　　　　　　　　　　　　　　图2

　　（3）如图3　　　　　　　　　　　（4）如图4

　
　　图3　　　　　　　　　　　　　　　图4

　　（5）如图5　　　　　　　　　　　（6）如图6

　
　　图5　　　　　　　　　　　　　　图6

　　说明：在数轴上表示不等式的解集时，要特别注意画线的方向和起点：大于向右画，小于向在画；不等号中含有等号起点画实心圆点，不含有等号起点画圆圈．

　　例3  分别用 的不等式表示下列用数轴表示的不等式的解集：

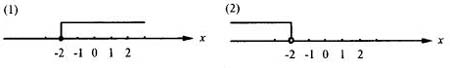
　　解：（1） ；　（2）

　　例4 求不等式 的正整数解．

　　解：由不等式的基本性质1，得 ，即 是不等式 的解集，因此不等式 的正整数解为1，2，共两个．

　　说明：本例是求不等式的特殊解（正整数解），可先利用不等式的基本性质求出不等式的所有解（即不等式的解集），然后从所有解中筛选出特殊解．

返回页首