第一节 不等式和它的基本性质

典型例题

　　例1 用“”或“”号填空

　　若 且 则：

　　（1） ______ ；　　　（2） _____ ；

　　（3） ____ ；　　　　　　（4） _____ ；

　　（5） _____ ；　　　（6） ___ ；

　　（7） ______ ；　　　　（8） _____ 。

　　解：（1）因为 ，根据不等式的性质1，有 ；

　　（2）因为 ，根据不等式的性质1，有 ；

　　（3）因为 ，根据不等式的性质2，有 ；

　　（4）因为 ，根据不等式的性质3，有 ，再由不等式性质1，有 ；

　　（5）因为 ，由不等式的性质1， ；

　　（6）因为 ，由不等式的性质1， ；

　　（7）因为 且 ，由不等式性质2知 ；

　　（8）因为 且 ，由不等式性质3，有

　　说明：解这类题应先观察不等号左右两边是由原来的不等式进行了什么样的变形得来的，弄清楚了，再对照不等式的性质，决定是否要改变不等号的方向。

　　例2  判断下列各题的结论是否正确，并说明理由．

　　（1）如果 ， ，那么 ；

　　（2）如果 ，那么 ；

　　（3）如果 ，那么 ；

　　（4）如果 ，且 ，那么 。

　　解：（1）不正确．因为当 或 时， 不成立；

　　（2）正确．因为 成立，必有 且 ，根据不等式基本性质2，得 ；

　　（3）正确．根据不等式基本性质1，由 ，两边都加上 ，得 ；

　　（4）不正确．因为 ，那么 有可能大于0，也有可能小于0，当 时，根据不等式基本性质3，两边同除以 得 。

　　说明：①注意 成立则隐含着 这个条件且

　　②要注意（4）小题中的条件“ ”的讨论，因为 代表有理数，所以 可能取正，也可能取负数．

　　例3 根据不等式的基本性质，把下列不等式化成 或 的形式．

　　（1） ；（2） ；（3） ；（4）

　　解：（l）根据不等式基本性质1，不等式两边都加上5，不等号的方向不改变，所以 ，即

　　（2）根据不等式基本性质1，不等式的两边都减去 ，不等式不改变方向，所以 ，即

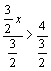　　（3）根据不等式基本性质2，不等式两边同除以 （或乘以 ），不等号不改变方向，所以 ，即

　　（4）根据不等式基本性质3，不等式两边同乘以－2（或除以－ ）；不等号改变方向，所以 ，即

　　说明：在运用不等式基本性质3时，一定不要忘记改变不等号的方向．

　　例4 用不等式表示

　　（1） 是正数；　　　　　（2） 与5的和是负数；

　　（3） 的一半不大于10；　（4） 的 与1的差是非负数．

　　分析：列不等式的关键是把数量关系中的“大于”、“是负数”、“不大于”、“是非负数”等文字语言正确地用数学符号表示出来，其中“非负数”是正数与零的统称．

　　解：（1） ；　　（2）

　　（3） ；　　（4）

返回页首